Umkehrfunktion: Unterschied zwischen den Versionen
(Lösung beigefügt und Applet) |
(Bilder eingefügt) |
||
| Zeile 15: | Zeile 15: | ||
Begründe, warum es sich bei dieser Kurve aber um keinen Graph einer Funktion handeln kann.}} | Begründe, warum es sich bei dieser Kurve aber um keinen Graph einer Funktion handeln kann.}} | ||
| − | + | ||
Die Umkehrfunktion der Exponentialfunktion hat eine große Bedeutung in der Mathematik und in den Naturwissenschaften und trägt die Bezeichnung '''Logarithmusfunktion'''. | Die Umkehrfunktion der Exponentialfunktion hat eine große Bedeutung in der Mathematik und in den Naturwissenschaften und trägt die Bezeichnung '''Logarithmusfunktion'''. | ||
| Zeile 21: | Zeile 21: | ||
{{Merksatz|MERK=Eine Funktion f: R<sup>+</sup> → R, f(x) = log<sub>a</sub>x heißt Logarithmusfunktion zur Basis a (a∈R<sup>+</sup>\{1})}} | {{Merksatz|MERK=Eine Funktion f: R<sup>+</sup> → R, f(x) = log<sub>a</sub>x heißt Logarithmusfunktion zur Basis a (a∈R<sup>+</sup>\{1})}} | ||
| + | |||
| + | [[Bild:Umkehrfunktion_Bild.png|right]] | ||
| + | |||
| + | |||
===Zusammenhang zwischen Logarithmusfunktionen und Exponentialfunktionen=== | ===Zusammenhang zwischen Logarithmusfunktionen und Exponentialfunktionen=== | ||
Da das Logarithmieren die Umkehroperation zum Exponenzieren ist, ist dementsprechend die Logarithmusfunktion die Umkehrfunktion (inverse Funktion) zur Exponentialfunktion. | Da das Logarithmieren die Umkehroperation zum Exponenzieren ist, ist dementsprechend die Logarithmusfunktion die Umkehrfunktion (inverse Funktion) zur Exponentialfunktion. | ||
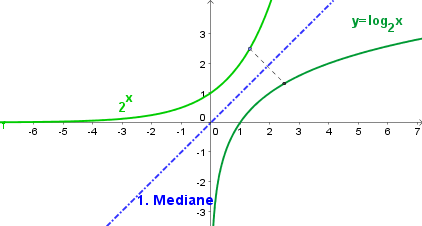
Der Graph einer Logarithmusfunktion geht durch Spiegeln an der 1.Mediane aus dem Graphen der entsprechenden Exponentialfunktion hervor. | Der Graph einer Logarithmusfunktion geht durch Spiegeln an der 1.Mediane aus dem Graphen der entsprechenden Exponentialfunktion hervor. | ||
| + | |||
| + | |||
Version vom 16. Januar 2010, 13:19 Uhr
Die Umkehrfunktion der Exponentialfunktion
Konstruiere die Umkehrfunktion zur Exponentialfunktion f(x) = axGehe dabei folgendermaßen vor:
Verändere die Basis a und bewege den Punkt P auf dem Graphen der Exponentialfunktion. Beobachte das Verhalten der beiden Funktionsgraphen und beschreibe in eigenen Worten, was dir auffällt (Definitionsmenge, Wertemenge, Monotonie). |
|
In der obigen Lösung wird bei der Exponentialfunktion f(x) = ax für die Basis a = 1 auch die gespiegelte Gerade gezeichnet. Begründe, warum es sich bei dieser Kurve aber um keinen Graph einer Funktion handeln kann. |
Die Umkehrfunktion der Exponentialfunktion hat eine große Bedeutung in der Mathematik und in den Naturwissenschaften und trägt die Bezeichnung Logarithmusfunktion.
|
Merke:
Eine Funktion f: R+ → R, f(x) = logax heißt Logarithmusfunktion zur Basis a (a∈R+\{1}) |
Zusammenhang zwischen Logarithmusfunktionen und Exponentialfunktionen
Da das Logarithmieren die Umkehroperation zum Exponenzieren ist, ist dementsprechend die Logarithmusfunktion die Umkehrfunktion (inverse Funktion) zur Exponentialfunktion. Der Graph einer Logarithmusfunktion geht durch Spiegeln an der 1.Mediane aus dem Graphen der entsprechenden Exponentialfunktion hervor.