SSS-Satz-1: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | [[Bild:Dreieck.png]] || Es war ganz schön umständlich in der letzten Aufgabe das rote Dreieck auf das orangefarbene abzubilden, indem man die Symmetrieachse und den Drehpunkt verschiebt, findest du nicht?<br />Es geht auch einfacher die Kongruenz von zwei Dreiecken nachzuweisen: Um ein Dreieck eindeutig festzulegen braucht man eine bestimmte Anzahl von Bestimmungsstücken. | + | | [[Bild:Dreieck.png]] || Es war ganz schön umständlich in der letzten Aufgabe das rote Dreieck auf das orangefarbene abzubilden, indem man die Symmetrieachse und den Drehpunkt verschiebt, findest du nicht? <br /> |
| + | Es geht auch einfacher die Kongruenz von zwei Dreiecken nachzuweisen: Um ein Dreieck eindeutig festzulegen braucht man eine bestimmte Anzahl von Bestimmungsstücken. | ||
|} | |} | ||
| + | |||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | Was denkst du, | + | Was denkst du, wie viele Angaben braucht man um ein Dreieck eindeutig konstruieren zu können? |
(3) (!2) (!4) (!1) (!5) (!6) | (3) (!2) (!4) (!1) (!5) (!6) | ||
| + | </div> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | <quiz> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Um ein Dreieck eindeutig festlegen zu können benötigt man also { drei } Bestimmungsstücke! | ||
| + | </quiz> | ||
| + | || [[Bild:Dreieck.png]] | ||
| + | |} | ||
| + | |||
| + | <br /> | ||
| + | Wir haben ja im vorherigen Lernpfad schon gesehen, dass ein Dreieck aus verschiedenen Teilen besteht, nämlich aus den Seiten und den Winkeln. | ||
| + | {{versteckt|[[Bild:Merke1.png]]}} <br /> | ||
| + | <u>Das heißt ja dann, dass man ein Dreieck festlegen kann wenn man folgende Bestimmungsstücke gegeben hat:</u> | ||
| + | <br />- alle drei Seitenlängen ''oder'' | ||
| + | <br />- 2 Seitenlängen und 1 Winkel ''oder'' | ||
| + | <br />- 1 Seitenlänge und 2 Winkel ''oder'' | ||
| + | <br />- alle 3 Winkel. | ||
| + | <br /><br /> | ||
| + | Das wollen wir uns jetzt einmal genauer anschauen! | ||
| + | <br /> | ||
| + | |||
| + | <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | [[Bild:KS_Dreieck2.JPG ]] || Wie konstruiert man ein Dreieck, von dem alle drei Seitenlängen gegeben sind? | ||
| + | |} | ||
| + | Wir wollen ein Dreieck konstruieren, von dem die Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm gegeben sind.<br /> | ||
| + | <quiz display="simple"> | ||
| + | {Als Erstes müssen wir überprüfen, ob das Dreieck mit diesen Maßen überhaupt konstruierbar ist. <br />Dies macht man hier mit der __________. } | ||
| + | - Seiten-Winkel-Beziehung | ||
| + | + Dreiecksungleichung | ||
| + | </quiz> | ||
| + | <br /> | ||
| + | <quiz> | ||
| + | { Das bedeutet, man überprüft ob die Summe von zwei Seitenlängen stets größer ist als die Länge der dritten Seite: <br /><small>(a = 7 cm, b = 5 cm und c = 3 cm)</small> | ||
| + | | type="{}" } | ||
| + | a + b > c, also 3 cm + 5 cm = { 8 } cm > 7 cm<br /> | ||
| + | b + c > a, also 5 cm + 7 cm = { 12 } cm > 3 cm<br /> | ||
| + | c + a > b, also 7 cm + 3 cm = { 10 } cm > 5 cm<br /> | ||
| + | </quiz> | ||
</div> | </div> | ||
| − | Wenn | + | Wenn wir das überprüft haben, geht es hier weiter zum [[2.Teil des 2.Lernpfades zur Dreieckskonstruktion]]. |
Version vom 12. Februar 2010, 11:01 Uhr
 |
Es war ganz schön umständlich in der letzten Aufgabe das rote Dreieck auf das orangefarbene abzubilden, indem man die Symmetrieachse und den Drehpunkt verschiebt, findest du nicht? Es geht auch einfacher die Kongruenz von zwei Dreiecken nachzuweisen: Um ein Dreieck eindeutig festzulegen braucht man eine bestimmte Anzahl von Bestimmungsstücken. |
Was denkst du, wie viele Angaben braucht man um ein Dreieck eindeutig konstruieren zu können? (3) (!2) (!4) (!1) (!5) (!6)
| |
|
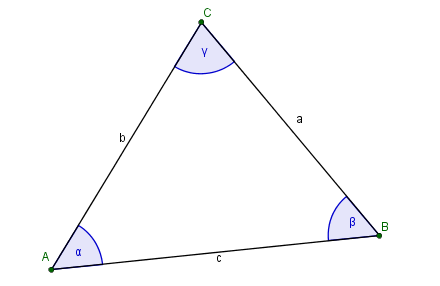
Wir haben ja im vorherigen Lernpfad schon gesehen, dass ein Dreieck aus verschiedenen Teilen besteht, nämlich aus den Seiten und den Winkeln.
Das heißt ja dann, dass man ein Dreieck festlegen kann wenn man folgende Bestimmungsstücke gegeben hat:
- alle drei Seitenlängen oder
- 2 Seitenlängen und 1 Winkel oder
- 1 Seitenlänge und 2 Winkel oder
- alle 3 Winkel.
Das wollen wir uns jetzt einmal genauer anschauen!
 |
Wie konstruiert man ein Dreieck, von dem alle drei Seitenlängen gegeben sind? |
Wir wollen ein Dreieck konstruieren, von dem die Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm gegeben sind.
Wenn wir das überprüft haben, geht es hier weiter zum 2.Teil des 2.Lernpfades zur Dreieckskonstruktion.
