SSS-Satz-1: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| Zeile 53: | Zeile 53: | ||
</div> | </div> | ||
| − | Wenn wir das überprüft haben, geht es hier weiter zum | + | <div algin="left">[[Benutzer:Kathrin_Fuchs/SSS_und_SWS/2.Teil des 2.Lernpfades|<math>\Rightarrow</math> Wenn wir das überprüft haben, geht es hier weiter zum 2.Teil des 2.Lernpfades zur Dreieckskonstruktion]]. </div> |
Version vom 15. Februar 2010, 10:12 Uhr
Was denkst du, wie viele Angaben braucht man um ein Dreieck eindeutig konstruieren zu können? (3) (!2) (!4) (!1) (!5) (!6)
|
Um ein Dreieck eindeutig festlegen zu können benötigt man also drei Bestimmungsstücke!
|

|
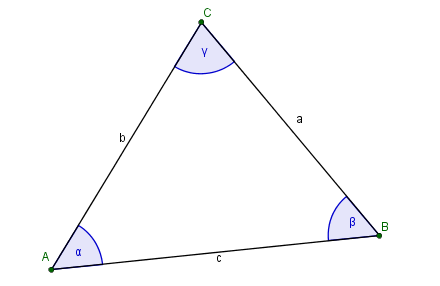
Wir haben ja im vorherigen Lernpfad schon gesehen, dass ein Dreieck aus verschiedenen Teilen besteht, nämlich aus den Seiten und den Winkeln.
Das heißt ja dann, dass man ein Dreieck festlegen kann wenn man folgende Bestimmungsstücke gegeben hat:
- alle drei Seitenlängen oder
- 2 Seitenlängen und 1 Winkel oder
- 1 Seitenlänge und 2 Winkel oder
- alle 3 Winkel.
Das wollen wir uns jetzt einmal genauer anschauen!

 Wenn wir das überprüft haben, geht es hier weiter zum 2.Teil des 2.Lernpfades zur Dreieckskonstruktion
Wenn wir das überprüft haben, geht es hier weiter zum 2.Teil des 2.Lernpfades zur Dreieckskonstruktion
