WSW-Satz-3: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: Bild:Dreieck.png So, jetzt vergleichen wir einmal die Konstruktionen und ihre Beschreibungen! <br /><br /> <div style="border: 2px solid #0000ee; background-color:...) |
K |
||
| Zeile 64: | Zeile 64: | ||
|} | |} | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | [[Bild:Dreieck.png]] || | + | | [[Bild:Dreieck.png]] || Das war spitze! |
|} | |} | ||
| + | |||
| + | [[Benutzer:Kathrin_Fuchs/WSW und SSW g/SSW g-Satz-1|<math>\Rightarrow</math> Lass uns jetzt den SSW<sub>g</sub>-Satz anschauen!]] | ||
Version vom 18. Februar 2010, 16:31 Uhr
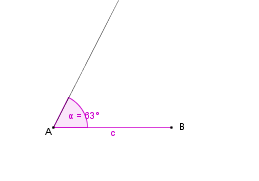
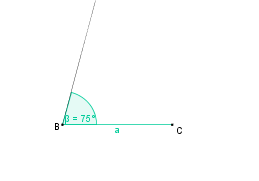
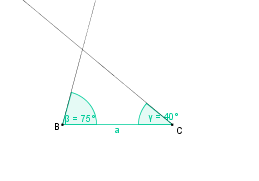
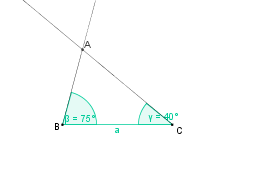
 So, jetzt vergleichen wir einmal die Konstruktionen und ihre Beschreibungen!
So, jetzt vergleichen wir einmal die Konstruktionen und ihre Beschreibungen!
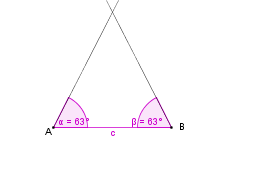
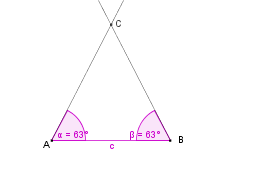
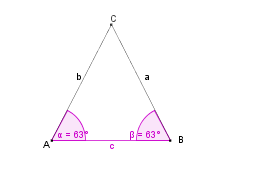
Konstruktionsbeschreibung zu a) mit c = 7 cm, 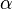 = 63° und
= 63° und 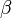 = 63°
= 63°
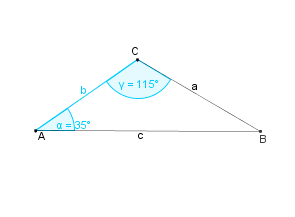
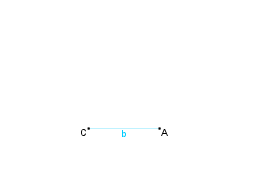
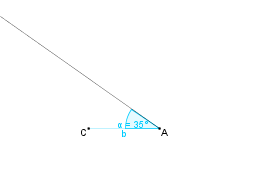
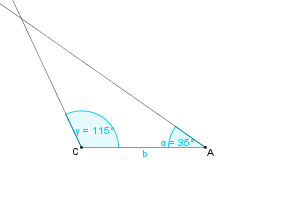
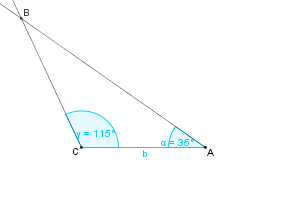
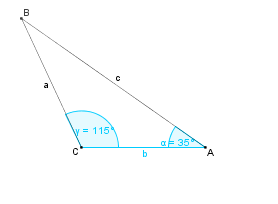
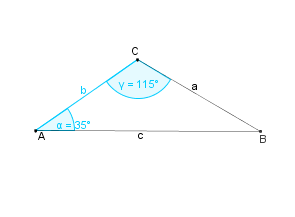
Konstruktionsbeschreibung zu b) mit b = 4,2 cm, 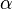 = 35° und
= 35° und 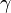 = 115°
= 115°
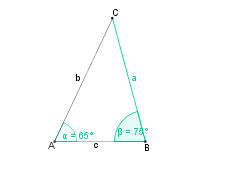
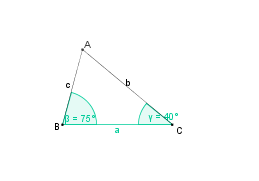
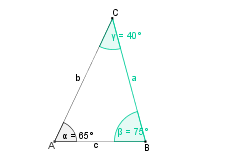
Konstruktionsbeschreibung zu c) mit a = 6,5 cm, 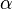 = 65° und
= 65° und 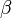 = 75°
= 75°
 |
Das war spitze! |
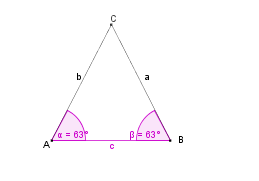
 63° gegen den Uhrzeigersinn ab.
63° gegen den Uhrzeigersinn ab.