Quadratische Funktionen und die Scheitelform: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Bestimmen der Scheitelpunktform mit variablem a)
Zeile 103: Zeile 103:
 
|}
 
|}
 
<br\>
 
<br\>
 +
Hast du die Paare gefunden? Dann gehts jetzt einen Schritt weiter.
 +
 +
<div algin="left">[[Variationen/Quadratische Funktionen2/Scheitelpunktform mit a|<math>\Rightarrow</math> Nächste Seite]]</div>
 +
<br>
 +
<div align="left">[[Variationen/Quadratische Funktionen2|<math>\Leftarrow</math> Zurück zur Übersicht]]</div>
 +
 
Jetzt kennst du dich mit der Scheitelpunktform schon recht gut aus. Allerdings haben wir bisher immer nur mit a=1 gearbeitet. Das ändern wir jetzt.  
 
Jetzt kennst du dich mit der Scheitelpunktform schon recht gut aus. Allerdings haben wir bisher immer nur mit a=1 gearbeitet. Das ändern wir jetzt.  
 
<br\>
 
<br\>

Version vom 22. Februar 2010, 17:11 Uhr

1. Fußball-WM 2006 - Wasserverbrauch 2. Quadratische Funktionen und Klippenspringen 3. Übungen 4. Quadratische Funktionen und Volleyball 5. Quadratische Funktionen und Fußball 6. Quadratische Funktionen und Basketball


Quadratische Funktionen und Basketball

Neben der Normalform gibt es auch die Scheitelpunktform.
Mit dieser kannst du in der nächsten Aufgabe experimentieren.


Aufgabe 14



Hast du deine ermittelten Wurfbahnen notiert?
Dann ist dir sicher aufgefallen, dass sich die Form unserer Gleichung stark verändert hat. Wie bereits erwähnt ist die Scheitelpunktform eine alternative Darstellung für die Normalform.
Quadratische Funktionen lassen sich auch so darstellen:

f(x) = a(x - xs)2 + ys


Vorsicht: Vor xs steht ein Minus. Ist xs also positiv, bleibt das Minus davor bestehen. Ist xs negativ, wird es zum Plus.

Der Parameter a bleibt also erhalten, b und c fallen weg. Dafür bekommen wir zwei Parameter hinzu. Jetzt kannst du noch einmal testen, für was xs und ys stehen.

Aufgabe 15

Verschiebe xs und ys auf dem nebenstehenden Arbeitsblatt. Was kannst du feststellen? Ordne jedem Fall eine Beispielgleichung zu.
A. f(x)=(x-2)²
B. f(x)=x²+2
C. f(x)=x²-2
D. f(x)=(x+2)²

Mache ich xs größer, so verschiebt sich der Scheitel nach rechts .
Eine Beispielfunktion dafür ist A .
Mache ich xs kleiner, so verschiebt sich der Scheitel nach links .
Eine Beispielfunktion dafür ist D .
Mache ich ys kleiner, so verschiebt sich der Scheitel nach unten .
Eine Beispielfunktion dafür ist C .
Mache ich ys größer, so verschiebt sich der Scheitel nach oben .
Eine Beispielfunktion dafür ist B .


Maehnrot.jpg
Merke:

xs hat immer den gleichen Wert wie die x-Koordinate des Scheitels und ys hat immer den gleichen Wert wie die y-Koordinate des Scheitels.

Aufgabe 16


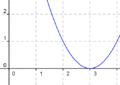
In dieser Funktion hat xs den Wert 2(Wert einfügen) und ys den Wert-4(Wert einfügen).


Aufgabe 17

In dem Memory sind Funktionsgleichungen und die Graphen der Funktionen versteckt. Finde die passenden Paare von Funktionsgeleichung und Graph! Dabei gilt immer a=1. Viel Vergnügen!

Geogebra17.1.png f(x)=(x+2)²+2
Geogebra17.2.png f(x)=(x+2)²-1
Geogebra17.3.png f(x)=(x-3)²
Geogebra17.4.png f(x)=(x-2)²+3
Geogebra17.5.png f(x)=(x-1)²-1
Geogebra17.6.png f(x)=x²-3


Hast du die Paare gefunden? Dann gehts jetzt einen Schritt weiter.


Jetzt kennst du dich mit der Scheitelpunktform schon recht gut aus. Allerdings haben wir bisher immer nur mit a=1 gearbeitet. Das ändern wir jetzt.

Bestimmen der Scheitelpunktform mit variablem a

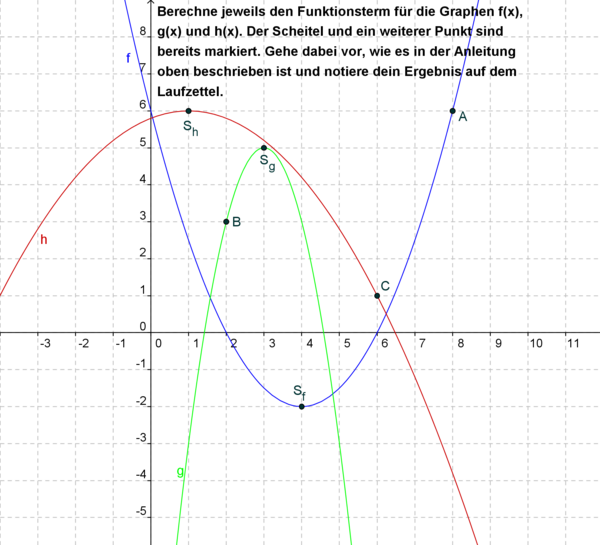
In dem Bild unten ist eine quadratische Funktion mit a ungleich 1 angezeigt. Auf dem Graphen der Funktion liegen zwei Punkte: S, der Scheitel, und P. Neben dem Graphen steht eine kurze Anleitung für die Berechnung von a und das Aufstellen der Funktionsgleichung. Vollziehe jeden Schritt der Anleitung nach. Danach sollst du eigenständig a bestimmen und Funktionsgleichungen aufstellen.

Geogebra18.png

Konntest du die Anleitung nachvollziehen? Mit diesem Verfahren kannst du nun jede quadratische Funktion bestimmen, wenn du ihren Scheitel kennst und die Koordinaten eines Punktes, der auf der Parabel der Funktion liegt.

Dann kannst du jetzt loslegen!

Aufgabe 18

Geogebra18.2.png

Hast du die Funktionsterme gefunden und auf deinem Laufzettel notiert?
Gut! Dann kannst du dich an die nächste Übung machen.

Aufgabe 19

In dieser Aufgabe sind jeweils die Koordinaten des Scheitelpunktes und die Koordinaten von einem weiteren Punkt auf der Parabel gegeben. Berechne jeweils den Funktionsterm auf dem Laufzettel und trage in die Lücke die Werte für a, xs und ys ein. Die Anleitung hilft dir wieder bei der Berechnung. Viel Erfolg!

a)

Eine Parabel hat ihren Scheitel S bei (-2/3) und einen Punkt P(2/14,2), der auf der Parabel liegt.


xs hat den Wert -2(Wert einfügen).
ys hat den Wert 3(Wert einfügen).
a hat den Wert 0,7(Wert einfügen).


c)

Eine Parabel hat ihren Scheitel S bei (3/-5) und einen Punkt P(6/4), der auf der Parabel liegt.


xs hat den Wert 3(Wert einfügen).
ys hat den Wert -5(Wert einfügen).
a hat den Wert 1(Wert einfügen).

b)

Eine Parabel hat ihren Scheitel S bei (-1/4) und einen Punkt P(2/-0,5), der auf der Parabel liegt.


xs hat den Wert -1(Wert einfügen).
ys hat den Wert 4(Wert einfügen).
a hat den Wert -0,5(Wert einfügen).


d)

Eine Parabel hat ihren Scheitel S bei (-4/6) und einen Punkt P(-6/-2), der auf der Parabel liegt.


xs hat den Wert -4(Wert einfügen).
ys hat den Wert 6(Wert einfügen).
a hat den Wert -2(Wert einfügen).

Von „http://dmuw.zum.de/index.php?title=Variationen/Quadratische_Funktionen2/Quadratische_Funktionen_und_die_Scheitelform&oldid=17104“