Endspurt: Unterschied zwischen den Versionen
(→Aufgabe x) |
|||
| Zeile 10: | Zeile 10: | ||
Das kannst du zunächst hier ausprobieren. | Das kannst du zunächst hier ausprobieren. | ||
| − | ===Aufgabe | + | ===Aufgabe 20=== |
<ggb_applet width="600" height="500" version="3.2" ggbBase64="UEsDBBQACAAIAAC5VjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vfbbtw2EH1uvoJQgcBuYVnUbbXIboImD4UBNzGwqQv0oQAlURJritqSlK319/RP+mMdktJeHMexk7ZIX1ba4XA4M2fOaLh4NbQcXVOpWCeWHvYDD1FRdCUT9dLrdXWSea9ePlvUtKtpLgmqOtkSvfQiP/SMvGcvn32zUE13gwi3KpeM3iy9inBFPaTWkpJSNZTqAznpB8YZkZt3+e+00Gq34IyciXUPp2jZg6xoy3Ompr+n5sCqExohxW4pOJ0a2eLU+rKgfcFZyYgw51nfQAmhG1bqBnTDNPZQQ1ndgL00iZy5outkudooTVs0/Eplt/Sy0I/TWTRPknkY4iSDbRu3EsfYj+bzaBbPszQM0gzCLAgHT6LAz/AsCWdJmkbhDM9C2DStRX6C4yAOwwwH6TzKUnc0vV5RrSHdCpGBqinmWrJy//1Mve54uU3TumNCvyFr3UuLVDSKVnpjDgMUpQnxB1FzOsrAl6KhxVXeDSuXt8iZfr9Z2y3Wnbx+0/FOIgkbkgQUxmfunlbH+LnVCqxOYDVGG8bodh3PQ6thn7l7Wi3OhHNtjBtPQeNgOoYpZARg3BTYlA5OcsqXnod6wfT59Eez4mqMFDv9t32bQ2Hvl83WJP6HTC5O79Tb4opKQbkrKgG49l2v0DXhE3TWj5IWrIW/bmFMCDFg/QwOOGlJa0knvx0rXLrsarBfuHfEi9PJCeODAl8LDfSGeLSJxbBPNx1gc6ZMqBxdArm5h0qizbIhEactBYZpWxqib6lkxTZNuWeOhvP68dQTHPqjQ7YTdJbU22Idt+1ggPVdlQXxQQVBB1g3BN58PNYJ2VB5ELS191NXjqePegpgAMWWickh1JLBUN68klx1vNd0VUBSxXlXEG07nsN/7A5hEBhd2BTFiXnbgCzNzFvFBrqjH2SP3QK85CCsXUXrBkpHUKUs7fQ+wYgA5C0c0G3WLk5ok9RYt+130kZriNySe1s4UG0OmE9CVNyFKEzuReig/P9DgHCyxcd69mR8guh/jQ+5iw/2068InpMdPJ+HTjyhE8ZfJzoDDCbKDD0uuwj0YPIZwGR1NByjJYKugb5DRwM6QVBqx78dgeAYfY9ix6M7+Fa9sD12C1blPTqmpyK+/8W13+Yt4sGDiL+rKkW1wecEW3Bwcm89hF+e6kdFvo9H0bUtESUSpIXlCzPK2AQyMwciEpiEukT0epJcOCPj1g8gsfPQNpUX3md9nVyuE2yTbR5Pz3WauGQ/xL0vy7UdApQ9LBx5l1ja3brdVsmNh2YWtgdHn2LE0qtHQtSOEAToMGxpkJt/8ISW9gg21P8eGz7e/x6LEHYpm80fYsMT6/nDbL6ng8ZjRp//0Xf6xSVMkj2M5KjsZdGgklH0muq//tSs7kWNTDN+/i0OXqyKhlEYOymMhxLEAslOw++Pkqwbp3L01lzLuLmcHcN0V1mtnJMeHk4BjFCmKV/34ko7vdsecVpT4VuNHMEVC2QSgV+UiYoUjXFDFQ0EMdm0qr9QqRGMWAjUagoVy7n2kQvqnt6oIXLvMA0PA71X2h/re4/HeYdksHd1VPA1rna3VHsfMteMadp3paiJ1LYXIVMnMx/uenOcRGk0D+MgGZso9sNZGuM4C6Msm8+ibJ93+zVxuj+M2wvreKl++TdQSwcIhFyoodkEAACGDwAAUEsBAhQAFAAIAAgAALlWPIRcqKHZBAAAhg8AAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAATBQAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | <ggb_applet width="600" height="500" version="3.2" ggbBase64="UEsDBBQACAAIAAC5VjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vfbbtw2EH1uvoJQgcBuYVnUbbXIboImD4UBNzGwqQv0oQAlURJritqSlK319/RP+mMdktJeHMexk7ZIX1ba4XA4M2fOaLh4NbQcXVOpWCeWHvYDD1FRdCUT9dLrdXWSea9ePlvUtKtpLgmqOtkSvfQiP/SMvGcvn32zUE13gwi3KpeM3iy9inBFPaTWkpJSNZTqAznpB8YZkZt3+e+00Gq34IyciXUPp2jZg6xoy3Ompr+n5sCqExohxW4pOJ0a2eLU+rKgfcFZyYgw51nfQAmhG1bqBnTDNPZQQ1ndgL00iZy5outkudooTVs0/Eplt/Sy0I/TWTRPknkY4iSDbRu3EsfYj+bzaBbPszQM0gzCLAgHT6LAz/AsCWdJmkbhDM9C2DStRX6C4yAOwwwH6TzKUnc0vV5RrSHdCpGBqinmWrJy//1Mve54uU3TumNCvyFr3UuLVDSKVnpjDgMUpQnxB1FzOsrAl6KhxVXeDSuXt8iZfr9Z2y3Wnbx+0/FOIgkbkgQUxmfunlbH+LnVCqxOYDVGG8bodh3PQ6thn7l7Wi3OhHNtjBtPQeNgOoYpZARg3BTYlA5OcsqXnod6wfT59Eez4mqMFDv9t32bQ2Hvl83WJP6HTC5O79Tb4opKQbkrKgG49l2v0DXhE3TWj5IWrIW/bmFMCDFg/QwOOGlJa0knvx0rXLrsarBfuHfEi9PJCeODAl8LDfSGeLSJxbBPNx1gc6ZMqBxdArm5h0qizbIhEactBYZpWxqib6lkxTZNuWeOhvP68dQTHPqjQ7YTdJbU22Idt+1ggPVdlQXxQQVBB1g3BN58PNYJ2VB5ELS191NXjqePegpgAMWWickh1JLBUN68klx1vNd0VUBSxXlXEG07nsN/7A5hEBhd2BTFiXnbgCzNzFvFBrqjH2SP3QK85CCsXUXrBkpHUKUs7fQ+wYgA5C0c0G3WLk5ok9RYt+130kZriNySe1s4UG0OmE9CVNyFKEzuReig/P9DgHCyxcd69mR8guh/jQ+5iw/2068InpMdPJ+HTjyhE8ZfJzoDDCbKDD0uuwj0YPIZwGR1NByjJYKugb5DRwM6QVBqx78dgeAYfY9ix6M7+Fa9sD12C1blPTqmpyK+/8W13+Yt4sGDiL+rKkW1wecEW3Bwcm89hF+e6kdFvo9H0bUtESUSpIXlCzPK2AQyMwciEpiEukT0epJcOCPj1g8gsfPQNpUX3md9nVyuE2yTbR5Pz3WauGQ/xL0vy7UdApQ9LBx5l1ja3brdVsmNh2YWtgdHn2LE0qtHQtSOEAToMGxpkJt/8ISW9gg21P8eGz7e/x6LEHYpm80fYsMT6/nDbL6ng8ZjRp//0Xf6xSVMkj2M5KjsZdGgklH0muq//tSs7kWNTDN+/i0OXqyKhlEYOymMhxLEAslOw++Pkqwbp3L01lzLuLmcHcN0V1mtnJMeHk4BjFCmKV/34ko7vdsecVpT4VuNHMEVC2QSgV+UiYoUjXFDFQ0EMdm0qr9QqRGMWAjUagoVy7n2kQvqnt6oIXLvMA0PA71X2h/re4/HeYdksHd1VPA1rna3VHsfMteMadp3paiJ1LYXIVMnMx/uenOcRGk0D+MgGZso9sNZGuM4C6Msm8+ibJ93+zVxuj+M2wvreKl++TdQSwcIhFyoodkEAACGDwAAUEsBAhQAFAAIAAgAALlWPIRcqKHZBAAAhg8AAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAATBQAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
| Zeile 19: | Zeile 19: | ||
Das war gar nicht so einfach. C | Das war gar nicht so einfach. C | ||
Daher gibt es auch eine rechnerische Lösung durch Umformung des Terms. Das ist gar nicht so schwer. Aber sieh dir selbst einmal die Anleitung dazu an: | Daher gibt es auch eine rechnerische Lösung durch Umformung des Terms. Das ist gar nicht so schwer. Aber sieh dir selbst einmal die Anleitung dazu an: | ||
| + | ::{|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="600"| | ||
| + | <div style="border: 2px solid #CD0000; background-color:#ffffff; padding:7px;"> | ||
<br\> | <br\> | ||
<big>'''Anleitung:'''</big> | <big>'''Anleitung:'''</big> | ||
<br\> | <br\> | ||
| − | Unsere Beispielfunktion in der '''Scheitelpunktform''' lautet wie in Aufgabe 20 '''f(x)=2(x-3)²+4'''<br\> | + | <br\> |
| + | Unsere Beispielfunktion in der '''Scheitelpunktform''' lautet wie in Aufgabe 20: '''f(x)=2(x-3)²+4'''<br\> | ||
<br\> | <br\> | ||
;1. Binomische Formel erkennen. <br\> | ;1. Binomische Formel erkennen. <br\> | ||
| Zeile 29: | Zeile 33: | ||
<br\> | <br\> | ||
;2. Binomische Formel auflösen.<br\> | ;2. Binomische Formel auflösen.<br\> | ||
| − | :Es handelt sich um die | + | :Es handelt sich um die 2. binomische Formel. Deshalb rechnen wir<br\> |
:f(x)=2(x²-6x+9)+4<br\> | :f(x)=2(x²-6x+9)+4<br\> | ||
<br\> | <br\> | ||
| Zeile 35: | Zeile 39: | ||
:f(x)=2x²-12x+18+4<br\> | :f(x)=2x²-12x+18+4<br\> | ||
:f(x)=2x²-12x+22 <br\> | :f(x)=2x²-12x+22 <br\> | ||
| − | + | <br\> | |
Und schon haben wir die '''Normalform f(x)=2x²-12x+22'''.<br\> | Und schon haben wir die '''Normalform f(x)=2x²-12x+22'''.<br\> | ||
| + | </div> | ||
| + | |} | ||
<br\> | <br\> | ||
Sieh noch einmal zur Aufgabe 20 zurück und überprüfe das Ergebnis. <br\> | Sieh noch einmal zur Aufgabe 20 zurück und überprüfe das Ergebnis. <br\> | ||
| − | Steht wirklich diese Funktionsgleichung neben dem roten Funktionsgraph? | + | Steht wirklich diese Funktionsgleichung neben dem roten Funktionsgraph?<br\> |
| + | <br\> | ||
| + | Nein!<br\> | ||
| + | Ja!<br\> | ||
| + | |||
| + | ===Aufgabe 21=== | ||
| + | |||
| + | Ordne die Funktionsgleichungen in der Normalform denjenigen in der Scheitelpunktform passend zu. | ||
| + | Forme dazu die Funktionsgleichung auf deinem Laufzettel nach der obigen Anleitung um. | ||
| + | Viel Erfolg! | ||
| + | |||
| + | <div class="zuordnungs-quiz"> | ||
| + | <big>'''Zuordnung'''</big><br> | ||
| + | Ordne richtig zu. | ||
| + | {| | ||
| + | | f(x) = 7(x + 1)<sup>2</sup> - 9 || f(x)= 7x<sup>2</sup> + 14x - 8 | ||
| + | |- | ||
| + | | f(x) = -0,5(x + 4)<sup>2</sup> - 2 || f(x)= -0,5x<sup>2</sup> + 4x + 6 | ||
| + | |} | ||
| + | </div> | ||
| + | <br> | ||
| + | Wenn du das geschafft hast, folgt die letzte Aufgabe!!!<br> | ||
| + | <br> | ||
| + | ===Aufgabe 22=== | ||
| + | <br> | ||
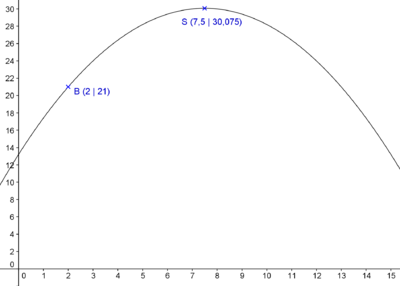
| + | Kannst du dich nach an den Anfang dieses Lernpfads erinnern? Wir haben von der Fußball-WM 2006 gesprochen und dem sich extrem verhaltendem Wasserverbrauch während der Halbzeitpause. Dazu hast du diesen Graph gezeichnet: | ||
| + | |||
| + | [[Bild:21.pgn|400px]] | ||
Version vom 22. Februar 2010, 23:55 Uhr
1. Fußball-WM 2006 - Wasserverbrauch | 2. Quadratische Funktionen und Klippenspringen | 3. Übungen | 4. Quadratische Funktionen und Volleyball | 5. Quadratische Funktionen und Fußball | Quadratische Funktionen und Basketball | Endspurt
Von der Scheitelpunktform zur Normalform
Wir haben in diesem Lernpfad schon einiges erarbeitet. Du hast die Normalform f(x)=ax²+bx+c und die Scheitelpunktform f(x)=a(x-xs)²+ys mit ihren Parametern kennengelernt. In diesen beiden Formen lassen sich Funktionsgleichungen von quadratischen Funktionen darstellen.
Doch wie genau hängen diese beiden Formen zusammen?
In diesem Teil des Lernpfades wollen wir einen Weg von der Scheitelpunktform zur Normalform finden.
Das kannst du zunächst hier ausprobieren.
Aufgabe 20
Hast du es geschafft, die beiden Funktionsgraphen aufeinanderzulegen?
Das war gar nicht so einfach. C
Daher gibt es auch eine rechnerische Lösung durch Umformung des Terms. Das ist gar nicht so schwer. Aber sieh dir selbst einmal die Anleitung dazu an:
Anleitung:
Unsere Beispielfunktion in der Scheitelpunktform lautet wie in Aufgabe 20: f(x)=2(x-3)²+4
- 1. Binomische Formel erkennen.
- Dir ist sicher schon aufgefallen, dass sich in der Scheitelpunktform eine binomische Formel versteckt!
- Hier heißt sie (x-3)².
- 2. Binomische Formel auflösen.
- Es handelt sich um die 2. binomische Formel. Deshalb rechnen wir
- f(x)=2(x²-6x+9)+4
- 3. Klammer auflösen und zusammenfassen.
- f(x)=2x²-12x+18+4
- f(x)=2x²-12x+22
Und schon haben wir die Normalform f(x)=2x²-12x+22.
- 1. Binomische Formel erkennen.
Sieh noch einmal zur Aufgabe 20 zurück und überprüfe das Ergebnis.
Steht wirklich diese Funktionsgleichung neben dem roten Funktionsgraph?
Nein!
Ja!
Aufgabe 21
Ordne die Funktionsgleichungen in der Normalform denjenigen in der Scheitelpunktform passend zu. Forme dazu die Funktionsgleichung auf deinem Laufzettel nach der obigen Anleitung um. Viel Erfolg!
Zuordnung
Ordne richtig zu.
| f(x) = 7(x + 1)2 - 9 | f(x)= 7x2 + 14x - 8 |
| f(x) = -0,5(x + 4)2 - 2 | f(x)= -0,5x2 + 4x + 6 |
Wenn du das geschafft hast, folgt die letzte Aufgabe!!!
Aufgabe 22
Kannst du dich nach an den Anfang dieses Lernpfads erinnern? Wir haben von der Fußball-WM 2006 gesprochen und dem sich extrem verhaltendem Wasserverbrauch während der Halbzeitpause. Dazu hast du diesen Graph gezeichnet: