Eigenschaften der zentrischen Streckung: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Zusammenfassung) |
(Stationen geändert) |
||
| Zeile 7: | Zeile 7: | ||
<br> | <br> | ||
| − | =1. Station: | + | =1. Station: Fixelemente= |
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
| − | + | :Für k<math>\not=</math>1 gilt: | |
| − | *''' | + | :Das Streckungszentrum Z ist Fixpunkt, da es immer auf sich selbst abgebildet wird. Deshalb sind |
| + | :alle Geraden die durch den Punkt Z verlaufen Fixgeraden. Sie werden bei einer zentrischen Streckung | ||
| + | :auf sich selbst abgebildet. | ||
| + | </div> | ||
| + | <br> | ||
| + | |||
| + | =2. Station: Geradentreue und Parallelentreue= | ||
| + | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
| + | *'''Geradentreue''' bedeutet, wenn das Bild einer Geraden ebenfalls auf eine Gerade abgebildet wird. | ||
| + | *'''Parallelentreue''' liegt vor, wenn das Bild einer parallelen Geraden wieder auf eine parallele Gerade abgebildet wird. | ||
</div> | </div> | ||
<br> | <br> | ||
| Zeile 20: | Zeile 29: | ||
<br> | <br> | ||
| − | = | + | =3. Station: Längentreue, Winkeltreue und Flächeninhaltstreue= |
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
| − | * | + | *'''Längentreue''' bedeutet, wenn alle Bildstrecken genauso lang sind wie die Urbildstrecken. |
| − | * | + | *Ebenso gilt für die '''Winkeltreue''', wenn alle Bildwinkel genauso groß sind wie die Urbildwinkel. |
| − | *''' | + | *'''Flächeninhaltstreue''' liegt vor, wenn der Flächeninhalt des Bildes genauso groß ist, wie der Flächeninhalt des Urbildes. |
</div> | </div> | ||
<br> | <br> | ||
| + | :In diesem Applet siehst du ein zentrisch gestrecktes Dreieck. Lass die das Winkelmaß, die Streckenlängen und | ||
| + | :den Flächeninhalt nacheinander anzeigen. Vergleiche die Werte und überlege, welche Eigenschaft zutrifft. | ||
<ggb_applet height="400" width="750" showResetIcon="true" filename="Porzelt_Winkel_Flächen_Längentreu.ggb" /> | <ggb_applet height="400" width="750" showResetIcon="true" filename="Porzelt_Winkel_Flächen_Längentreu.ggb" /> | ||
<br> | <br> | ||
| − | + | :Durch Umformung kannst du herausfinden, wie der Flächeninhalt des zentrisch gestreckten Dreiecks zu berechnen ist. | |
| + | :Setze dafür die richtigen Aussagen in die passenden Lücken ein: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
A<sub><math>\Delta</math>ABC</sub> = 0,5 ∙ <span style="text-decoration: overline;">AB</span> ∙ h <br> | A<sub><math>\Delta</math>ABC</sub> = 0,5 ∙ <span style="text-decoration: overline;">AB</span> ∙ h <br> | ||
| Zeile 40: | Zeile 52: | ||
<br> | <br> | ||
| − | = | + | =4. Station: Kreistreue= |
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
| − | : | + | :'''Kreistreue''' bedeutet, wenn das Bild eines Kreises ebenfalls ein Kreis ist. |
</div> | </div> | ||
<br> | <br> | ||
| + | :Mit Hilfe dieses Applets kannst du einen Kreis zentrisch strecken. Finde heraus, ob die zentrische Streckung kreistreu ist. | ||
<ggb_applet height="350" width="650" showResetIcon="true" filename="Porzelt_Kreistreue.ggb" /> | <ggb_applet height="350" width="650" showResetIcon="true" filename="Porzelt_Kreistreue.ggb" /> | ||
| − | = | + | =5. Station: Zusammenfassung= |
:Übertrage die Zusammenfassung in dein Heft. | :Übertrage die Zusammenfassung in dein Heft. | ||
<div style="border: 2px solid #FF0000; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #FF0000; background-color:#ffffff; padding:7px;"> | ||
| Zeile 59: | Zeile 72: | ||
</div> | </div> | ||
| − | = | + | =6. Station: Übung= |
Version vom 2. Juli 2009, 09:59 Uhr
 Lernpfad
|
1. Station: Fixelemente
- Für k
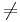1 gilt:
- Das Streckungszentrum Z ist Fixpunkt, da es immer auf sich selbst abgebildet wird. Deshalb sind
- alle Geraden die durch den Punkt Z verlaufen Fixgeraden. Sie werden bei einer zentrischen Streckung
- auf sich selbst abgebildet.
2. Station: Geradentreue und Parallelentreue
- Geradentreue bedeutet, wenn das Bild einer Geraden ebenfalls auf eine Gerade abgebildet wird.
- Parallelentreue liegt vor, wenn das Bild einer parallelen Geraden wieder auf eine parallele Gerade abgebildet wird.
- Hier siehst du einen Punkt P der auf der Geraden g verläuft. P wird durch zentrische Streckung mit dem Zentrum Z
- auf den Punkt P' abgebildet.
- Schritt 1: Bewege den Punkt P auf der Geraden g und beobachte die Spur die der Punkt P' hinterlässt. Was stellst du fest?
- Schritt 2: Änder den Streckungsfaktor und wiederhole Schritt 1.
3. Station: Längentreue, Winkeltreue und Flächeninhaltstreue
- Längentreue bedeutet, wenn alle Bildstrecken genauso lang sind wie die Urbildstrecken.
- Ebenso gilt für die Winkeltreue, wenn alle Bildwinkel genauso groß sind wie die Urbildwinkel.
- Flächeninhaltstreue liegt vor, wenn der Flächeninhalt des Bildes genauso groß ist, wie der Flächeninhalt des Urbildes.
- In diesem Applet siehst du ein zentrisch gestrecktes Dreieck. Lass die das Winkelmaß, die Streckenlängen und
- den Flächeninhalt nacheinander anzeigen. Vergleiche die Werte und überlege, welche Eigenschaft zutrifft.
- Durch Umformung kannst du herausfinden, wie der Flächeninhalt des zentrisch gestreckten Dreiecks zu berechnen ist.
- Setze dafür die richtigen Aussagen in die passenden Lücken ein:
A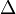
ABC = 0,5 ∙ AB ∙ h
A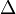A'B'C' = 0,5 ∙ A'B' ∙ h'
A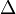A'B'C' = 0,5 ∙ |k| ∙ AB ∙ |k| ∙ h
A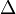A'B'C' = |k|² ∙ 0,5 ∙ AB ∙ h
A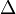A'B'C' = |k|² ∙ A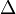ABC
4. Station: Kreistreue
- Kreistreue bedeutet, wenn das Bild eines Kreises ebenfalls ein Kreis ist.
- Mit Hilfe dieses Applets kannst du einen Kreis zentrisch strecken. Finde heraus, ob die zentrische Streckung kreistreu ist.
5. Station: Zusammenfassung
- Übertrage die Zusammenfassung in dein Heft.
Eigenschaften der zentrischen Streckung
Jede Gerade die durch das Zentrum Z verläuft, wird auf sich selbst abgebildet. Sie ist eine Fixgerade.
Jede Gerade, die nicht durch das Zentrum Z verläuft, wird auf eine parallele Bildgerade abgebildet. Sie ist parallelentreu.
Die Bildstrecke ist |k|-mal so lang wie die Urstrecke. Sie ist also nicht längentreu.
Die zentrische Streckung ist geradentreu, winkeltreu und kreistreu.
Der Flächeninhalt der Bildfigur beträgt das |k|²-fache des Flächeninhalts der Urfigur. (A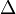A'B'C' = |k|² ∙ A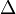ABC)
Die zentrische Streckung ist deshalb nicht flächeninhaltstreu.
