7a der St.-Ursula-Schule:Lernpfad Drehung Aufgabe D: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(table+ table+) |
|||
| Zeile 1: | Zeile 1: | ||
| + | <div style="border: 3px solid green; padding:7px;"> | ||
| + | # Wiederholung der wichtigen Begriffe | ||
| + | # Drehung als Doppelachsenspiegelung | ||
| + | # '''''Drehung: Konstruktion''''' | ||
| + | # Eigenschaften der Drehung | ||
| + | </div> | ||
| + | |||
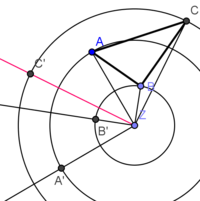
| + | '''''Im Folgenden wird gezeigt, wie man die Drehung um 90° (gegen den Uhrzeigersinn) speziell für ein Dreieck durchführen kann.''''' | ||
| + | |||
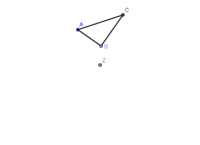
| + | Gegeben ist ein Dreieck ABC (Uhrfigur) und ein Punkt Z (Drehzentrum). Z liegt außerhalb von Dreieck ABC. | ||
| + | |||
| + | Gesucht: Bildfigur vom Dreieck ABC, die durch eine Drehung um Z mit Winkel <math>\alpha</math> = 90° entsteht. | ||
| + | |||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ '''''Konstruktion: Drehung um 90°''''' | |+ '''''Konstruktion: Drehung um 90°''''' | ||
| Zeile 9: | Zeile 23: | ||
| [[Bild:Ak_konstruktion_drehung.png|200px|border]] | | [[Bild:Ak_konstruktion_drehung.png|200px|border]] | ||
| [[Bild:Ak_konstruktion_drehung1.png|200px|right|border]] | | [[Bild:Ak_konstruktion_drehung1.png|200px|right|border]] | ||
| − | | | + | | |
| + | '''Hinweis:''' ''Versuche zuerst jedes Konstruktionsbild selbstständig nachzuvollziehen und wenn du nicht weiter weißt, dann klicke auf "anzeigen"'' | ||
| + | |||
| + | Lösung: | ||
| + | <popup> | ||
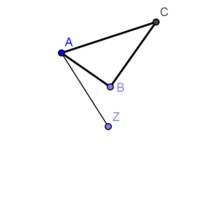
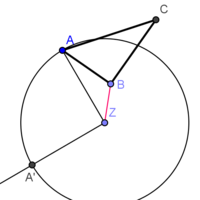
| + | * [AZ] - Verbindungsstrecke zwischen Eckpunkt A und Drehpunkt Z</popup> | ||
|- | |- | ||
| [[Bild:Ak_konstruktion_drehung2.png|200px|border]] | | [[Bild:Ak_konstruktion_drehung2.png|200px|border]] | ||
| [[Bild:Ak_konstruktion_drehung3.png|right|200px|border]] | | [[Bild:Ak_konstruktion_drehung3.png|right|200px|border]] | ||
| − | | | + | | <popup> |
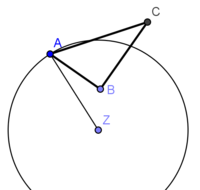
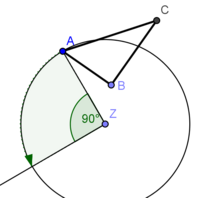
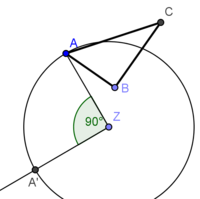
| + | * Kreis um Z mit Radius <span style="text-decoration: overline;">ZA</span> | ||
| + | * Abtragen des Drehwinkels <math>\alpha</math> = 90° (mit Geodreieck)</popup> | ||
|- | |- | ||
| − | |||
| [[Bild:Ak_konstruktion_drehung4.png|right|200px|border]] | | [[Bild:Ak_konstruktion_drehung4.png|right|200px|border]] | ||
| − | | | + | | |
| + | | <popup> | ||
| + | * Der Punkt A´ liegt auf dem Kreis um Z mit Radius <span style="text-decoration: overline;">ZA</span> und gehört dem zweiten Schenkel des Winkels AZA´= 90° an | ||
| + | * '''Der Punkt A´ ist der Bildbunkt von A'''</popup> | ||
|- | |- | ||
| [[Bild:Ak_konstruktion_drehung5.png|200px|border]] | | [[Bild:Ak_konstruktion_drehung5.png|200px|border]] | ||
| [[Bild:Ak_konstruktion_drehung6.png|right|200px|border]] | | [[Bild:Ak_konstruktion_drehung6.png|right|200px|border]] | ||
| − | | | + | | <popup> |
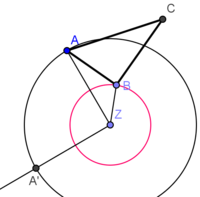
| + | * [BZ] - Verbindungsstrecke zwischen Eckpunkt B und Drehpunkt Z | ||
| + | * Kreis um Z mit Radius <span style="text-decoration: overline;">ZB</span></popup> | ||
|- | |- | ||
| [[Bild:Ak_konstruktion_drehung7.png|200px|border]] | | [[Bild:Ak_konstruktion_drehung7.png|200px|border]] | ||
| [[Bild:Ak_konstruktion_drehung8.png|right|200px|border]] | | [[Bild:Ak_konstruktion_drehung8.png|right|200px|border]] | ||
| − | | | + | | <popup> |
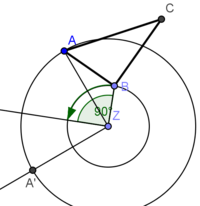
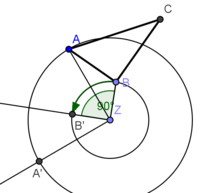
| + | * Abtragen des Drehwinkels BZB´ = <math>\alpha</math> = 90° (mit Geodreieck) | ||
| + | * Der Punkt B´ ist der Schnittpunkt des Kreises um Z mit Radius <span style="text-decoration: overline;">ZB</span> und des zweiten Schenkels von Winkel BZB´ | ||
| + | * '''B´ ist der Bildpunkt von B''' </popup> | ||
|- | |- | ||
| [[Bild:Ak_konstruktion_drehung9.png|200px|border]] | | [[Bild:Ak_konstruktion_drehung9.png|200px|border]] | ||
| [[Bild:Ak_konstruktion_drehung10.png|right|200px|border]] | | [[Bild:Ak_konstruktion_drehung10.png|right|200px|border]] | ||
| − | | | + | | <popup> |
| + | * [CZ] - Verbindungsstrecke zwischen Eckpunkt C und Drehpunkt Z | ||
| + | * Kreis um Z mit Radius <span style="text-decoration: overline;">ZC</span></popup> | ||
|- | |- | ||
| [[Bild:Ak_konstruktion_drehung11.png|200px|border]] | | [[Bild:Ak_konstruktion_drehung11.png|200px|border]] | ||
| [[Bild:Ak_konstruktion_drehung12.png|right|200px|border]] | | [[Bild:Ak_konstruktion_drehung12.png|right|200px|border]] | ||
| − | | | + | | <popup> |
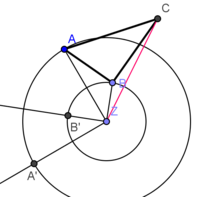
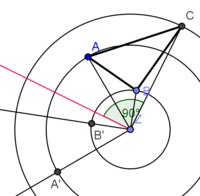
| + | * Abtragen des Drehwinkels CZC´ = <math>\alpha</math> = 90° (mit Geodreieck) | ||
| + | * Der Punkt C´ ist der Schnittpunkt des Kreises um Z mit Radius <span style="text-decoration: overline;">ZC</span> und des zweiten Schenkels von Winkel CZC´ | ||
| + | * '''C´ ist der Bildpunkt von C'''</popup> | ||
|- | |- | ||
| [[Bild:Ak_konstruktion_drehung13.png|200px|border]] | | [[Bild:Ak_konstruktion_drehung13.png|200px|border]] | ||
| [[Bild:Ak_konstruktion_drehung14.png|200px|border]] | | [[Bild:Ak_konstruktion_drehung14.png|200px|border]] | ||
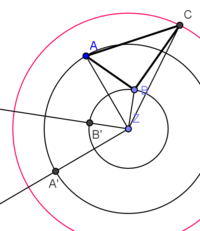
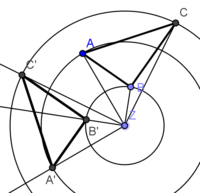
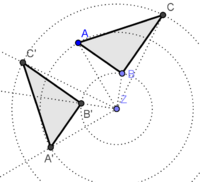
| − | | | + | |<popup> |
| + | * Das Dreieck A´B´C´ist die gesuchte Bildfigur</popup> | ||
|} | |} | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''''Schön! Nun weißt du, wie man so eine Drehung konstruieren kann! Dann kannst du jetzt versuchen, mit Hilfe von Frgen auf der nächsten Seite die Eigenschaften der Drehung zu entdecken!''''' | ||
| + | |||
| + | [[7a_der_St.-Ursula-Schule:Lernpfad_Drehung_Fragen| '''''Weiter zu den Fragen''''']] | ||
| + | ---- | ||
| + | |||
| + | [[7a der St.-Ursula-Schule:Lernpfad Drehung Aufgabe C| '''''Zurück''''']] | ||
| + | |||
| + | [[7a der St.-Ursula-Schule| '''''Zurück zu 7a''''']] | ||
Aktuelle Version vom 17. Juni 2010, 09:36 Uhr
- Wiederholung der wichtigen Begriffe
- Drehung als Doppelachsenspiegelung
- Drehung: Konstruktion
- Eigenschaften der Drehung
Im Folgenden wird gezeigt, wie man die Drehung um 90° (gegen den Uhrzeigersinn) speziell für ein Dreieck durchführen kann.
Gegeben ist ein Dreieck ABC (Uhrfigur) und ein Punkt Z (Drehzentrum). Z liegt außerhalb von Dreieck ABC.
Gesucht: Bildfigur vom Dreieck ABC, die durch eine Drehung um Z mit Winkel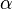 
= 90° entsteht.
| Konstruktionsbilder | Konstruktionsbeschreibung
| |
|---|---|---|
|
 |
Hinweis: Versuche zuerst jedes Konstruktionsbild selbstständig nachzuvollziehen und wenn du nicht weiter weißt, dann klicke auf "anzeigen" Lösung: |
|
 |
|
 |
||
|
 |
|
|
 |
|
|
 |
|
|
 |
|
|
|
Schön! Nun weißt du, wie man so eine Drehung konstruieren kann! Dann kannst du jetzt versuchen, mit Hilfe von Frgen auf der nächsten Seite die Eigenschaften der Drehung zu entdecken!
