Würfel- und Quaderoberfläche: Unterschied zwischen den Versionen

Version vom 21. Juli 2010, 10:24 Uhr

Das Quadernetz Schaue dir das Applet doch mal genauer an. Du hast hier gesehen, dass ein Netz ensteht, wenn du den Quader auseinanderklappst. So ein Netz kann dir bei der Berrechnung der Oberfläche helfen. Schaue dir dazu doch die nächste Aufgabe an. Beachte: Ein Würfel ist ein Spezialfall vom Quader, bei dem alle Kantenlängen gleich groß sind!

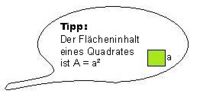
Die Würfeloberfläche (O_W) Jonas hat in Mathe Hausaufgaben aufbekommen. Er soll eine quadratische Verpackung aufschneiden und die Oberfläche bestimmen. Überlege dir zusammen mit deiner Gruppe wie groß die Fläche ist. Rechnet sie auf einem Blatt Papier aus. Die Maße könnt ihr dem Bild entnehmen.(!40 cm²)(54 cm²)(!18 cm²)(!36 cm²) Wie groß ist diese Oberfläche, wenn die Kantenlänge a beträgt?(!O_W = 6·a) (O_W = 6·a²) (!O_W = 6·a+a) (!O_W = a·a)

Das Baumhaus Beachte: In die grünen Felder ziehst du die passende Lösung von unten rein. In die weißen Felder trägst du deine Lösung selbst ein. Rechne im Kopf. Hanna hat von ihrem Papa ein gebaut bekommen. Bevor er es in dem Baum fest verankert, möchte sie es noch gerne verschönern. Türen und Fenster hat der Papa noch nicht ausgepart. Sie hat sich dazu entschlossen es von außen ganz in anzumalen. Sie braucht für 54(m²) Farbe. Eine Flasche Farbe reicht für 10 m², somit müssen ihre Eltern 6(Flaschen) Farbe kaufen.

Quaderoberfläche (O_Q) Bsp.:Ich habe ein Würfelnetz . Ich lege mir die Flächen so , dass die Flächen a² sechs mal nebeneinander liegen. O_W ist dann 6·a² Rechts im Applet kannst auch du die Flächen verschieben. Gehe wie im Beispiel vor und kontrolliere, welche Formeln stimmen. Es können mehrere Lösungen stimmen. Ist die Formel O_Q = 6·a² richtig? (!ja) (nein) Ist die Formel O_Q = 2·a·b+2·b·c+2·a·c richtig? (ja) (!nein) Ist die Formel O_Q = 2·(a·b+b·c+a·c) richtig? (ja) (!nein) Ist die Formel O_Q = 6·a·b·c richtig? (!ja) (nein)

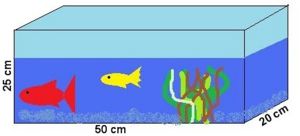
Das Auqarium Beachte: Berechne die Aufgaben auf ein Platt Papier. Tipp: Der Flächeninhalt für ein Rechteck mit den Kanten a und b ist a·b. Joans muss sein mit einer Wäremeschutzfolie bekleben, damit es den bei diesem heißen Sommer nicht zu warm wird. Es reicht, wenn er die Decke und die Seitenwändebeklebt. Jonas braucht ür die linke und rechte Seite zwei Folien die zusammen 1000 (cm²) groß sind, zwei die je 1250 cm² groß sind und eine die 1000(cm²) groß ist. Insgesamt braucht Jonas Folie für 4500(cm²).

@@ Zeile 13: / Zeile 13: @@
 ::<ggb_applet height="500" width="900" filename="SchiebereglerNetz2.ggb"/>
 <br>
-Du hast hier gesehen, dass ein Netz ensteht, wenn du den Quader auseinanderklappst. So ein Netz kann dir bei der Berrechnung der Oberfläche helfen. Schaue dir dazu doch die nächste Aufgabe an.
+Du hast hier gesehen, dass ein Netz ensteht, wenn du den Quader auseinanderklappst. So ein Netz kann dir bei der Berrechnung der Oberfläche helfen. Schaue dir dazu doch die nächste Aufgabe an. Beachte: Ein Würfel ist ein Spezialfall vom Quader, bei dem alle Kantenlängen gleich groß sind!
 </div>
 |}
@@ Zeile 22: / Zeile 22: @@
 | width="550" |
 <div style="padding:10px;background:#ffffff;border:1px ;">
 ==='''<u>Die Würfeloberfläche (O<sub>W</sub>)</u>'''===
 <br>