Mathematisches Modellieren: Unterschied zwischen den Versionen
(→Ergebnis erklären) |
(kat) |
||
| Zeile 105: | Zeile 105: | ||
[[/Radfahren um den Bodensee| Zur Aufgabe: Radfahren um den Bodensee]] | [[/Radfahren um den Bodensee| Zur Aufgabe: Radfahren um den Bodensee]] | ||
| + | |||
| + | |||
| + | |||
| + | [[Kategorie:Modellierung]] | ||
Version vom 6. Januar 2011, 01:02 Uhr
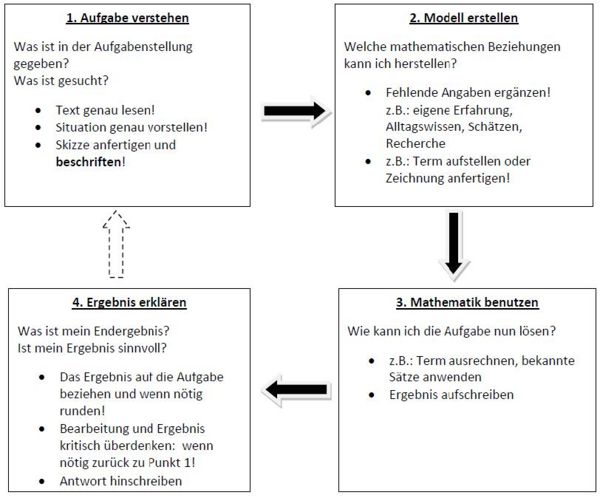
Modellierungskreislauf
Beispielaufgabe: Außenputz
Aufgabe verstehen
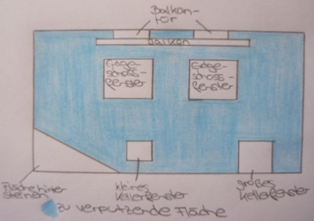
Zunächst mache ich mir eine Vorstellung darüber, wie die zu verputzende Wand später aussehen soll und fertige dazu eine Skizze an
Nun überlege ich welche Teile der Wand verputzt werden sollen bzw. nicht verputzt werden sollen. Nicht verputzt werden:
- mit Holz verkleidete Fläche
- Fenster
- Balkonboden
- Balkontüren
- Fläche hinter Steinen
Ich habe nun also eine genaue Vorstellung von der Aufgabe.
Aber wie berechne ich nun die gesuchte Fläche?
Modell erstellen
Um die Flächen berechnen zu können überlege ich welche mathematische Formen, deren Flächeninhalt ich berechnen kann, die Wand am besten beschreiben. Für die Wandfläche, Fenster, Balkonboden und Balkontüren sind Rechtecke am naheliegensten. Für die Fläche hinter den Steinen eignet sich ein Dreieck. Somit ergibt sich folgende Skizze:
Zu Berechnen ist also:
gesamte Wandfläche - (kleines Kellerfenster + großes Kellerfenster + 2·Erdgeschossfenster + Balkon + 2·Balkontür + Fläche hinter Steinen)
Eine Rechtecksfläche berechne ich durch die Formel: Länge · Breite
Die Dreiecksfläche durch: 0,5 · Grundfläche · Höhe
Da es sich hier um ein rechtwinkliges Dreieck handelt kann ich für die Grundfläche und Höhe die Abmessungen der entsprechenden Außenseite des Hauses verwenden.
Aber wie soll ich die Fläche ohne Längenangaben berechnen?
Ich betrachte nochmals das Bild in der Angabe! Ich weiß, dass eine normale Raumhöhe etwa 2,60m entspricht. Also nehme ich diesen Wert von 2,60m für die Raumhöhe des Hauses an und messe diese im Bild. Dies ist gut möglich, da man zwischen den einzelnen Mauersteinen die Decke gut erkennen kann. Ich messe hier 2,6cm. Der Rest des Hauses wird auch noch vermessen.
Nun habe ich alle benötigten Maße aus dem Bild gemessen.
Mathematik benutzen
Die im Bild gemessenen Maße kann ich nun in die entsprechenden realen Längen umrechnen
2,6cm 
2,6m
1cm 1m
Wandfläche bis Dachschräge:
Länge: 9,5cm 9,50m
Breite: 4,8cm 4,80m
großes Kellerfenster:
Länge: 1,1cm 1,10m
Breite: 1,2cm 1,20m
kleines Kellerfenster:
Länge: 0,9cm 0,90m
Breite: 0,7cm 0,70m
Erdgeschossfenster:
Länge: 1,7cm 1,70m
Breite: 1,4cm 1,40m
Balkonboden:
Länge: 5,3cm 5,30m
Breite: 0,3cm 0,30m
Balkontür:
Länge: 1,2cm 1,20m
Breite: 0,5cm 0,50m
Fläche hinter Steinen:
Länge: 3,0cm 3,00m
Höhe: 1,5cm 1,50m
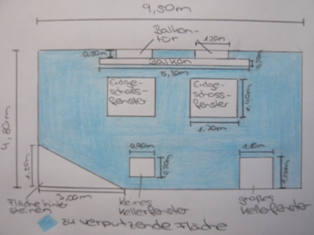
Nun kann ich die Maße in meine Skizze eintragen:
Da ich nun alle nötigen Maße habe, kann ich mit der Flächenberechnung beginnen:
Flächenberechnung:
gesamte Wandfläche - (kleines Kellerfenster + großes Kellerfenster + 2·Erdgeschossfenster + Balkon + 2·Balkontür + Fläche hinter Steinen)
Zu Berechnen ist somit folgender Term:
9,50m · 4,80m - (0,90m · 0,70m + 1,10m · 1,20m + 2 · 1,70m · 1,40m + 5,30m · 0,30m + 2 · 1,20m · 0,50m + 0,5 · 3,00m · 1,50m)
= 45,60m² - (0,63m² + 1,32m² + 4,76m² + 1,59m² + 1,20m² + 2,25m²)
= 45,60m² - 11.75m²
= 33,85m²
Ergebnis erklären
Beim oben abgebildetet Haus muss eine Fläche von etwa 34 m² verputzt werden.
Die Maßeinheit Quadratmeter gibt einen Flächeninhalt an, was auch zu berechnen war. Die Größenordnung der Fläche von etwa 34 m² ist realistisch.
Man hat jetzt einen Anhaltspunkt, wenn man zum Beispiel Putz kaufen will. Hier muss man sich natürlich bewusst sein, dass man für einige Quadratmeter mehr Putz kaufen muss als für 34 m², denn während der Modellierung habe ich Annahmen getroffen und die Situation vereinfacht. Man muss also aufrunden und auch an kleine Ungenauigkeiten denken, denn am Ende darf man auf keinen Fall zu wenig Putz haben.
