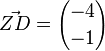Aufgaben 7. Klasse/Drehung/Seite 3: Unterschied zwischen den Versionen
(overrightarrow durch vec ersetzt) |
|||
| Zeile 8: | Zeile 8: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | '''Die Koordinaten vom Vektor <math>\ | + | '''Die Koordinaten vom Vektor <math>\vec{ZD}</math> hast du ja schon berechnet.''' |
<br /> | <br /> | ||
<span style="color:#CD2626">'''Zur Erinnerung:'''</span> | <span style="color:#CD2626">'''Zur Erinnerung:'''</span> | ||
<popup name="Vektoren"> | <popup name="Vektoren"> | ||
| − | <big>Z = (1/5)</big>; <math>\ | + | <big>Z = (1/5)</big>; <math>\vec{ZD}={-4\choose -1}</math> |
</popup> | </popup> | ||
<br /> | <br /> | ||
| − | ''' 1.) Gib nun die Koordinaten des Punktes D‘ an und berechne den Vektor <math>\ | + | ''' 1.) Gib nun die Koordinaten des Punktes D‘ an und berechne den Vektor <math>\vec{ZD'}</math>! Gehe so vor, wie in Teilaufgabe b)! ''' |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 26: | Zeile 26: | ||
{| | {| | ||
|- | |- | ||
| − | | <math>\ | + | | <math>\vec{ZD'}</math> = [[Bild:klammerMM.gif]] || |
{| | {| | ||
|- | |- | ||
| Zeile 50: | Zeile 50: | ||
'''3.) Schauen wir uns die Eigenschaften der 90° Drehung nun nochmal genauer an! Versuche dafür die verdrehten Wörter zu entschlüsseln!''' | '''3.) Schauen wir uns die Eigenschaften der 90° Drehung nun nochmal genauer an! Versuche dafür die verdrehten Wörter zu entschlüsseln!''' | ||
| − | <u>Hinweis:</u> Betrachte die beiden Vektoren <math>\ | + | <u>Hinweis:</u> Betrachte die beiden Vektoren <math>\vec{ZD}</math> und <math>\vec{ZD'}</math> genauer! |
<div class="schuettel-quiz"> | <div class="schuettel-quiz"> | ||
| − | Bei einer Drehung um 90° '''vertauschen''' sich die Koordinaten von '''Urvektor''' <math>\ | + | Bei einer Drehung um 90° '''vertauschen''' sich die Koordinaten von '''Urvektor''' <math>\vec{ZD}</math> und '''Bildvektor''' <math>\vec{ZD'}</math> und das Vorzeichen der |
x – '''Koordinate''' des Bildvektors wird '''umgedreht'''. | x – '''Koordinate''' des Bildvektors wird '''umgedreht'''. | ||
Aktuelle Version vom 20. März 2012, 19:23 Uhr
Teilaufgabe c)
Du siehst hier eine feste Drehung des Flugdrachens, die du nicht verändern kannst!
Die Koordinaten vom Vektor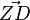 
hast du ja schon berechnet.
Zur Erinnerung:
1.) Gib nun die Koordinaten des Punktes D‘ an und berechne den Vektor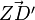 
! Gehe so vor, wie in Teilaufgabe b)!
D' = (2(x- Koordinate)/1(y- Koordinate))
=  |
|
|
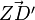2.) Um wie viel Grad wurde somit der Drachen im Applet gedreht? Zur Verdeutlichung kannst du dir die beiden Tipps "Vektorkoordinaten" und "Vektoren" im Applet anschauen!
90(°)
Toll gemacht!! Das war schwer!
3.) Schauen wir uns die Eigenschaften der 90° Drehung nun nochmal genauer an! Versuche dafür die verdrehten Wörter zu entschlüsseln!
Hinweis: Betrachte die beiden Vektoren 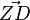und 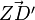genauer!
Bei einer Drehung um 90° vertauschen sich die Koordinaten von Urvektor 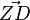und Bildvektor 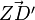und das Vorzeichen der
x – Koordinate des Bildvektors wird umgedreht.
