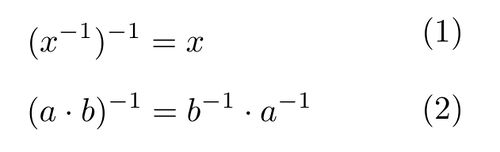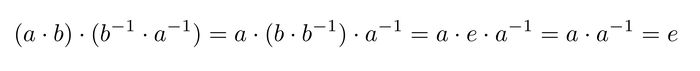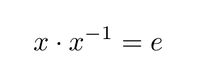Doppelte Invertierung eines Gruppenelements/Shoes and Socks: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 16: | Zeile 16: | ||
==Aspekte== | ==Aspekte== | ||
| − | *Wir | + | *Wir können die Aussage (2) auch nachrechnen: |
[[Datei:Shoes and Socks 4.jpg|center|700px]] | [[Datei:Shoes and Socks 4.jpg|center|700px]] | ||
| − | :Somit ist <math> (a \cdot b) \cdot (b^{-1} \cdot a^{-1}) = e </math>, d.h. | + | :Somit ist <math> (a \cdot b) \cdot (b^{-1} \cdot a^{-1}) = e </math>, d.h. <math> (b^{-1} \cdot a^{-1}) </math> ist ein rechtsinverses Element von <math> (a \cdot b) </math>. |
| − | :Wir wissen (siehe [[Abschwächung der Gruppendefinition|Abschwächung der Gruppendefinition]]), dass in einer Gruppe die Begriffe rechts- und linksinvers zusammenfallen. | + | :Wir wissen (siehe [[Abschwächung der Gruppendefinition|Abschwächung der Gruppendefinition]]), dass in einer Gruppe die Begriffe rechts- und linksinvers zusammenfallen. D.h. <math> (b^{-1} \cdot a^{-1}) </math> muss auch linksinverses Element von <math> (a \cdot b) </math> sein. |
| − | :Genauso wissen wir mit der Aussage über die [[Eindeutigkeit des neutralen Elements und der inversen Elemente in einer Gruppe|Eindeutigkeit der inversen Elemente in einer Gruppe]], dass | + | :Genauso wissen wir mit der Aussage über die [[Eindeutigkeit des neutralen Elements und der inversen Elemente in einer Gruppe|Eindeutigkeit der inversen Elemente in einer Gruppe]], dass ein inverses Element eines Gruppenelements eindeutig bestimmt ist. Somit ist <math> (b^{-1} \cdot a^{-1}) </math> das einzige zu <math> (a \cdot b </math>) inverse Element. |
*Genauso gilt: | *Genauso gilt: | ||
| − | [[Datei:Shoes and Socks 5.jpg|center| | + | [[Datei:Shoes and Socks 5.jpg|center|200px]] |
:Wir können die Aussage so lesen: <math> x </math> ist linksinvers zu <math> x^{-1} </math>. Genauso können wir die Aussage auch so lesen: <math> x^{-1} </math> ist rechtsinvers zu <math> x </math>. | :Wir können die Aussage so lesen: <math> x </math> ist linksinvers zu <math> x^{-1} </math>. Genauso können wir die Aussage auch so lesen: <math> x^{-1} </math> ist rechtsinvers zu <math> x </math>. | ||
| − | :Also ist <math> x </math> ist | + | :Also ist <math> x </math> das inverse Element von <math> x^{-1} </math>, denn ist ein Gruppenelement linksinvers zu einem anderen, dann auch rechtsinvers zu diesem. Also ein inverses Element. Es kann aber nur ein inverses Element geben. |
| − | *Die zweite Aussage kann man sich gut merken. Wenn man <math> a </math> für "Socken anziehen" und <math> b </math> für "Schuhe anziehen" nimmt. Dann ist die "inverse Operation" zu "Socken und Schuhe anziehen". | + | *Shoes and Socks: Die zweite Aussage kann man sich gut merken. Wenn man <math> a </math> für "Socken anziehen" und <math> b </math> für "Schuhe anziehen" nimmt. Dann ist die "inverse Operation" zu "Socken und Schuhe anziehen": "Socken und Schuhe ausziehen". Aber bevor man die Socken ausziehen kann, muss man zuerst die "Schuhe ausziehen" <math> b^{-1} </math> und dann kann man die "Socken ausziehen" <math> a^{-1} </math>. |
[[Kategorie:Beweis Gruppe|Beweis]] | [[Kategorie:Beweis Gruppe|Beweis]] | ||
Version vom 26. November 2018, 20:03 Uhr
Aussage
Sei 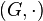 eine Gruppe (abgeschlossene zweistellige Verknüpfung + Assoziativität + neutrales Element + inverse Elemente), dann gilt für alle
eine Gruppe (abgeschlossene zweistellige Verknüpfung + Assoziativität + neutrales Element + inverse Elemente), dann gilt für alle 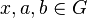 :
:
Beweis
1. Doppelte Invertierung eines Gruppenelements
2. Shoes and Socks
Aspekte
- Wir können die Aussage (2) auch nachrechnen:
- Somit ist
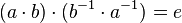 , d.h.
, d.h. 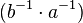 ist ein rechtsinverses Element von
ist ein rechtsinverses Element von 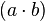 .
.
- Wir wissen (siehe Abschwächung der Gruppendefinition), dass in einer Gruppe die Begriffe rechts- und linksinvers zusammenfallen. D.h.
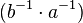 muss auch linksinverses Element von
muss auch linksinverses Element von 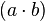 sein.
sein.
- Genauso wissen wir mit der Aussage über die Eindeutigkeit der inversen Elemente in einer Gruppe, dass ein inverses Element eines Gruppenelements eindeutig bestimmt ist. Somit ist
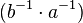 das einzige zu
das einzige zu 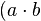 ) inverse Element.
) inverse Element.
- Genauso gilt:
- Wir können die Aussage so lesen:
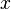 ist linksinvers zu
ist linksinvers zu 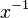 . Genauso können wir die Aussage auch so lesen:
. Genauso können wir die Aussage auch so lesen: 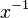 ist rechtsinvers zu
ist rechtsinvers zu 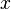 .
.
- Also ist
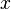 das inverse Element von
das inverse Element von 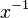 , denn ist ein Gruppenelement linksinvers zu einem anderen, dann auch rechtsinvers zu diesem. Also ein inverses Element. Es kann aber nur ein inverses Element geben.
, denn ist ein Gruppenelement linksinvers zu einem anderen, dann auch rechtsinvers zu diesem. Also ein inverses Element. Es kann aber nur ein inverses Element geben.
- Shoes and Socks: Die zweite Aussage kann man sich gut merken. Wenn man
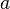 für "Socken anziehen" und
für "Socken anziehen" und 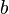 für "Schuhe anziehen" nimmt. Dann ist die "inverse Operation" zu "Socken und Schuhe anziehen": "Socken und Schuhe ausziehen". Aber bevor man die Socken ausziehen kann, muss man zuerst die "Schuhe ausziehen"
für "Schuhe anziehen" nimmt. Dann ist die "inverse Operation" zu "Socken und Schuhe anziehen": "Socken und Schuhe ausziehen". Aber bevor man die Socken ausziehen kann, muss man zuerst die "Schuhe ausziehen" 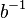 und dann kann man die "Socken ausziehen"
und dann kann man die "Socken ausziehen" 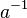 .
.