Untergruppenkriterium: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „==Aussage== Sei <math> (G, \ast) </math> eine Gruppe und U eine Teilmenge von G, also <math> U \subset G </math>. Dann gilt: Datei:Untergruppenkriterium 1.j…“) |
|||
| Zeile 1: | Zeile 1: | ||
==Aussage== | ==Aussage== | ||
| − | Sei <math> (G, \ast) </math> eine Gruppe und U eine Teilmenge von G, also <math> U \subset G </math>. Dann gilt: | + | Sei <math> (G, \ast) </math> eine Gruppe und U eine Teilmenge von G, also <math> U \subset G </math> und <math> a, b \in U </math>. Dann gilt: |
[[Datei:Untergruppenkriterium 1.jpg|center|700px]] | [[Datei:Untergruppenkriterium 1.jpg|center|700px]] | ||
| Zeile 7: | Zeile 7: | ||
Was bedeutet "mit der eingeschr\"ankten Verkn\"upfung von G auf U"? G ist eine Gruppe, d.h. es gibt eine Verknüpfung auf G, also eine Abbildung <math> \ast : G \times G \to G </math>. <br> | Was bedeutet "mit der eingeschr\"ankten Verkn\"upfung von G auf U"? G ist eine Gruppe, d.h. es gibt eine Verknüpfung auf G, also eine Abbildung <math> \ast : G \times G \to G </math>. <br> | ||
| − | Wir haben eine Abbildung, d.h. wir können Einschränkungen dieser Abbildung betrachten. In unserem Fall betrachten wir <math> \ast \ | + | Wir haben eine Abbildung, d.h. wir können Einschränkungen dieser Abbildung betrachten. In unserem Fall betrachten wir <math> \ast \vert_{ U \times U }</math>. |
Ist U mit dieser Einschränkung eine Gruppe (Abgeschlossenheit + Assoziativität + neutrales Element + inverse Elemente), dann sagen wir: U ist eine Untergruppe von G und schreiben: <math> U \leq G </math> | Ist U mit dieser Einschränkung eine Gruppe (Abgeschlossenheit + Assoziativität + neutrales Element + inverse Elemente), dann sagen wir: U ist eine Untergruppe von G und schreiben: <math> U \leq G </math> | ||
| Zeile 14: | Zeile 14: | ||
Es liegt eine Äquivalenz vor, d.h. wir müssen zwei Implikationen zeigen: | Es liegt eine Äquivalenz vor, d.h. wir müssen zwei Implikationen zeigen: | ||
| − | + | "<math> \Rightarrow </math>" : | |
| + | |||
| + | Sei U eine Gruppe. U ist eine Gruppe und damit abgeschlossen. Also gilt <math> \ast ( U \times U ) \subset U </math>, also gilt <math> \forall a, b \in U </math> : <math> a \ast b \in U </math>. | ||
| + | U ist eine Gruppe, d.h. es existieren inverse Elemente. Die Verknüpfung in U ist die Einschränkung von G auf U. Die inversen Element sind eindeutig bestimmt. [[Eindeutigkeit des neutralen Elements und der inversen Elemente in einer Gruppe|(Eindeutigkeit der inversen Elemente in einer Gruppe)]]. D.h. für ein <math>a \in U </math> gibt es nur ein <math> g \in G </math> mit <math> \ast (a, g) = e </math>. U ist eine Gruppe, d.h. es gibt für alle <math> u \in U </math> | ||
| + | Also ist für ein Element <math> a \in U </math> | ||
==Aspekte== | ==Aspekte== | ||
[[Kategorie:Beweis Gruppe|Beweis]] | [[Kategorie:Beweis Gruppe|Beweis]] | ||
__NOTOC__ | __NOTOC__ | ||
Version vom 27. November 2018, 17:03 Uhr
Aussage
Sei 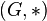 eine Gruppe und U eine Teilmenge von G, also
eine Gruppe und U eine Teilmenge von G, also 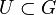 und
und 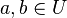 . Dann gilt:
. Dann gilt:
Definitionen
Was bedeutet "mit der eingeschr\"ankten Verkn\"upfung von G auf U"? G ist eine Gruppe, d.h. es gibt eine Verknüpfung auf G, also eine Abbildung 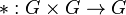 .
.
Wir haben eine Abbildung, d.h. wir können Einschränkungen dieser Abbildung betrachten. In unserem Fall betrachten wir 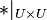 .
Ist U mit dieser Einschränkung eine Gruppe (Abgeschlossenheit + Assoziativität + neutrales Element + inverse Elemente), dann sagen wir: U ist eine Untergruppe von G und schreiben:
.
Ist U mit dieser Einschränkung eine Gruppe (Abgeschlossenheit + Assoziativität + neutrales Element + inverse Elemente), dann sagen wir: U ist eine Untergruppe von G und schreiben: 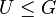
Beweis
Es liegt eine Äquivalenz vor, d.h. wir müssen zwei Implikationen zeigen:
" " :
" :
Sei U eine Gruppe. U ist eine Gruppe und damit abgeschlossen. Also gilt 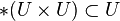 , also gilt
, also gilt 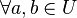 :
: 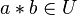 .
U ist eine Gruppe, d.h. es existieren inverse Elemente. Die Verknüpfung in U ist die Einschränkung von G auf U. Die inversen Element sind eindeutig bestimmt. (Eindeutigkeit der inversen Elemente in einer Gruppe). D.h. für ein
.
U ist eine Gruppe, d.h. es existieren inverse Elemente. Die Verknüpfung in U ist die Einschränkung von G auf U. Die inversen Element sind eindeutig bestimmt. (Eindeutigkeit der inversen Elemente in einer Gruppe). D.h. für ein 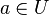 gibt es nur ein
gibt es nur ein 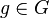 mit
mit 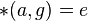 . U ist eine Gruppe, d.h. es gibt für alle
. U ist eine Gruppe, d.h. es gibt für alle 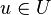 Also ist für ein Element
Also ist für ein Element