Zerlegungsgleichheit von Figuren: Unterschied zwischen den Versionen
(Bild geändert Aufgabe2) |
(→Aufgabe 3: Ergänzungsgleiche Figuren) |
||
| Zeile 145: | Zeile 145: | ||
===Aufgabe 3: Ergänzungsgleiche Figuren=== | ===Aufgabe 3: Ergänzungsgleiche Figuren=== | ||
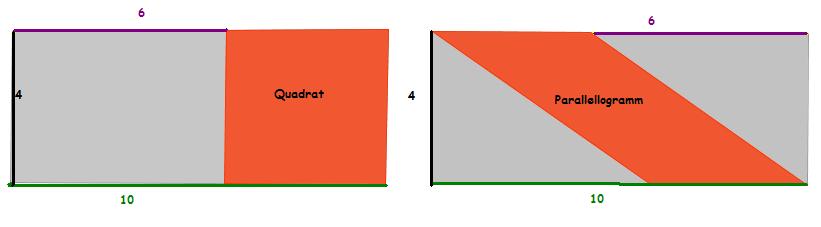
| + | :'''Zwei Rechtecken mit der Länge 10cm und der Breite 4cm ist ein Quadrat und ein Parallelogramm einbeschrieben.'''<br> | ||
| + | :'''Was haben Quadrat und Parallelogramm gemeinsam?''' | ||
| − | + | [[Bild:Ebert_Scherungsaufgabe.jpg|center]] | |
| − | [[Bild:Ebert_QuadratundParallelogramm.jpg|center]] | + | '''Tipp:'''{{versteckt| Überlege, wie man das linke und das rechte Rechteck geeignet zerlegen kann.}}<br> |
| + | <quiz display="simple"> | ||
| + | |||
| + | {Haben Quadrat und Parallelogramm den gleichen Umfang?} | ||
| + | -ja | ||
| + | +nein | ||
| + | |||
| + | {Besitzen Quadrat und Parallelogramm den gleichen Flächeninhalt?} | ||
| + | +ja | ||
| + | -nein | ||
| + | |||
| + | {Sind Quadrat und Parallelogramm ergänzungsgleiche Figuren?} | ||
| + | +ja | ||
| + | -nein | ||
| + | |||
| + | {Sind Quadrat und Parallelogramm zerlegungsgleich?} | ||
| + | -nein | ||
| + | +ja | ||
| + | |||
| + | </quiz> | ||
| + | |||
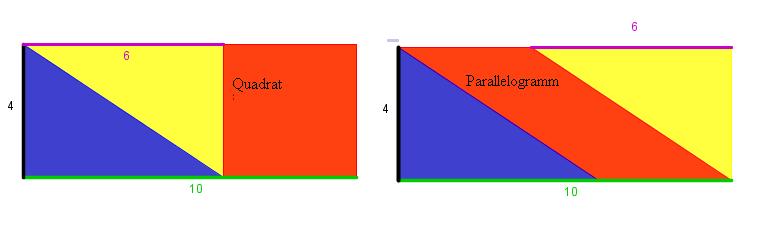
| + | :'''Bist Du ganz sicher, dass Du den Hinweis brauchst?'''<br> | ||
| + | {{versteckt| | ||
| + | [[Bild:Ebert_QuadratundParallelogramm.jpg|center]]}} | ||
Version vom 14. Juli 2009, 17:59 Uhr
Zerlegungsgleichheit von Figuren
1.Station: Einführung
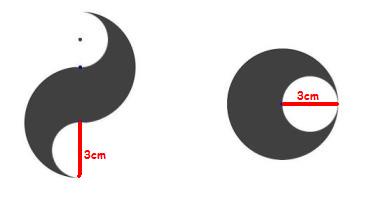
Kapitän Check Aufgabe: Welche ist die größte Insel?
- Aufgabenstellung:
- Du siehst hier die 3 schwarzen Inseln. Darunter befinden sich alle Teilfiguren, mit denen man die Inseln vollständig zusammensetzen kann. Du kannst diese Teilfiguren auf die Inseln ziehen.
- Überlege Dir zunächst selbst, wo die nächste Teilfigur platziert werden könnte.
- Wenn Du eine Hilfestellung brauchst, dann Klicke die Kontrollkästchen an.
- Was fällt Dir auf? Welche ist die größte Insel?
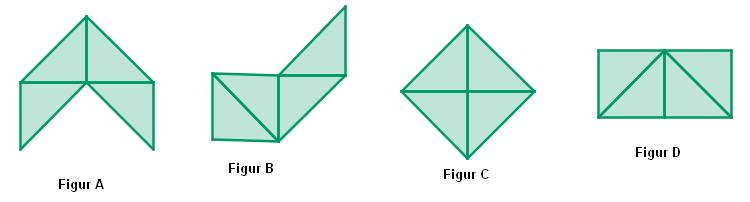
Trage hier den Namen der Insel ein, die am größten ist:
Die größte Insel ist Isola Bella (entweder Isola Grande, Isola Bella oder Isola Piccola eintragen)
Begründe Deine Antwort, warum ist diese Insel die größte?
Die Figuren A und C sind gleich groß, da sie mit sechs Teilfiguren ausgelegt werden können, die jeweils kongruent zueinander sind.
Figur B kann mit einer Teilfigur, dem grauen Dreieck mehr ausgelegt werden, deshalb ist sie die größte der drei Inseln.
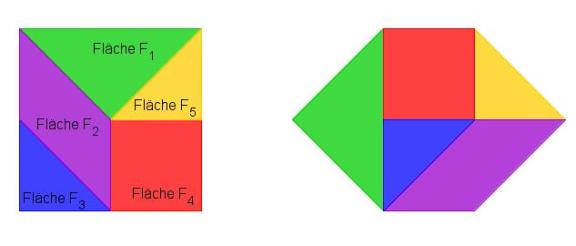
2.Station: Das Prinzip der Zerlegungsgleichheit
FQuadrat = F1 + F2 + F3 + F4 + F5 =FSechseck |
- Nils fasst hier Dein Ergebnis kurz zusammen. Übertrage es in Dein Heft:
- Maja möchte Dir auch noch etwas sagen:
- Hierzu siehst Du ein kleines Beispiel:
- Kannst Du zeigen, dass die beiden folgenden Figuren den gleichen Flächeninhalt haben?
Bist Du sicher,dass Du den Hinweis brauchst?
Hier findest du den Hinweis
3. Station: Zusammenfassung
- Übertrage folgende Definition in Dein Heft:
4.Station: Anwendung
- Maja weiß jetzt, wozu man die Zerlegungsgleichheit von Figuren nutzen kann. Lies, was sie Dir erzählen möchte:
5.Station:Übung
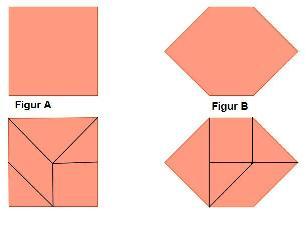
Aufgabe 1
Begründe, warum die folgenden Figuren A und B den gleichen Flächeninhalt besitzen:
Aufgabe 2: Ergänzungsgleiches Parallelogramme
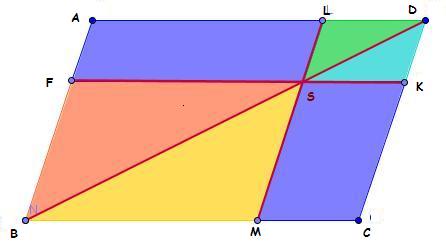
Maja zerschneidet das Parallelogramm ABCE entlang den roten Linien. [BD] ist die Diagonale, [FK] die eine Parallele zur Seite [BC] und [LM] eine Parallele zu den anderen [AB] Die Strecken schneiden sich im Punkt S
Warum besitzen die beiden blauen enstehenden Teilparallelogramme AFSL und MCKS den gleichen Flächeninhalt? Orientiere Dich dabei an den Fragen: Wie teilt die Diagonale das Parallelogramm ABCE? Hast Du schon die Dreiecke betrachtet? Warum sind diese Dreiecke kongruent zueinander?
Aufgabe 3: Ergänzungsgleiche Figuren
- Zwei Rechtecken mit der Länge 10cm und der Breite 4cm ist ein Quadrat und ein Parallelogramm einbeschrieben.
- Was haben Quadrat und Parallelogramm gemeinsam?
Tipp:
- Bist Du ganz sicher, dass Du den Hinweis brauchst?