Übung zum Flächeninhalt Parallelogramm: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K (→Übung 3 für Profis: Wie ändert sich der Flächeninhalt?) |
(Tabelle vereinfacht. Applet dazu) |
||
| Zeile 13: | Zeile 13: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Der Flächeninhalt des Zimmers NILS beträgt: '''96 (m²)'''<br> | Der Flächeninhalt des Zimmers NILS beträgt: '''96 (m²)'''<br> | ||
| − | Der Flächeninhalt des Zimmers | + | Der Flächeninhalt des Zimmers SDEU beträgt: '''32(m²)'''<br> |
| − | Der Flächeninhalt des Zimmers | + | Der Flächeninhalt des Zimmers DLAG beträgt: '''32 (m²)''' |
</div> | </div> | ||
<br> | <br> | ||
| Zeile 27: | Zeile 27: | ||
:'''''In der Tabelle sind Werte verschiedener Größen von Parallelogrammen angegeben.'''''<br> | :'''''In der Tabelle sind Werte verschiedener Größen von Parallelogrammen angegeben.'''''<br> | ||
:'''''Arbeitsauftrag:''''' <br> | :'''''Arbeitsauftrag:''''' <br> | ||
| − | :''''' | + | :'''''Vervollständige die Tabelle und erstelle das Parallelogramm! '''' |
| − | <div class="lueckentext-quiz"> | + | <div class="lueckentext-quiz"> |
{| {{Prettytable}} | {| {{Prettytable}} | ||
|- style="background-color:#8DB6CD" | |- style="background-color:#8DB6CD" | ||
| − | ! Parallelogramm !! | + | ! Parallelogramm !! Grundseite g !! Höhe h !! Flächeninhalt F |
|- | |- | ||
| − | | A ||3 cm || 2cm || '''6 cm²''' | + | | A ||3 cm || 2cm || '''6 cm²''' |
|- | |- | ||
| − | | B ||3 cm || '''3cm''' || 9 cm² | + | | B ||3 cm || '''3cm''' || 9 cm² |
|- | |- | ||
| − | | C || ''' | + | | C || '''4 cm''' || 4,5cm || 18cm² |
| + | |- | ||
| + | | D || 5 || '''4cm''' || 20cm² | ||
|} | |} | ||
</div> | </div> | ||
| − | + | ||
| − | < | + | |
| + | |||
| + | <ggb_applet height="300" width="600" filename="Ebert_ParallelogrammVariationsaufgabe.ggb" /> | ||
| + | |||
| + | |||
---- | ---- | ||
| Zeile 66: | Zeile 72: | ||
- Der Flächeninhalt wird '''halbiert''' | - Der Flächeninhalt wird '''halbiert''' | ||
- Der Flächeninhalt wird '''vervierfacht''' | - Der Flächeninhalt wird '''vervierfacht''' | ||
| − | + | - Der Flächeninhalt '''gedrittelt''' | |
| − | + | + Der Flächeninhalt wird '''bleibt gleich''' | |
- Der Flächeninhalt wird '''verdoppelt''' | - Der Flächeninhalt wird '''verdoppelt''' | ||
Version vom 22. Juli 2009, 19:36 Uhr
Übung 1 zum Warmwerden: Berechne den Flächeninhalt
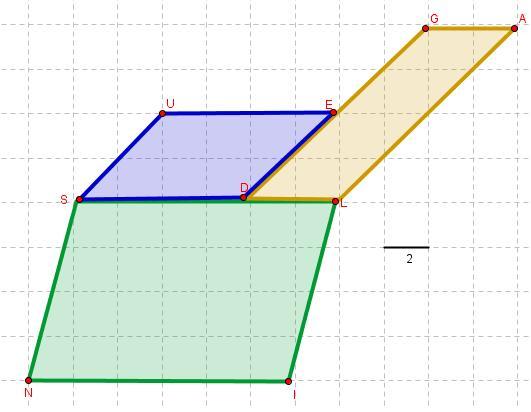
- Maja und Nils haben eine gemeinsame Wohnung. Sie wollen die Wohnfläche berechnen, die Du hier siehst:
Hinweis:
Ein Kästchen enstpricht 2 Metern
- Wie groß sind die einzelnen Zimmer?
Der Flächeninhalt des Zimmers NILS beträgt: 96 (m²)
Der Flächeninhalt des Zimmers SDEU beträgt: 32(m²)
Der Flächeninhalt des Zimmers DLAG beträgt: 32 (m²)
Übung 2 für Könner: Berechne die fehlenden Maße
- In der Tabelle sind Werte verschiedener Größen von Parallelogrammen angegeben.
- Arbeitsauftrag:
- Vervollständige die Tabelle und erstelle das Parallelogramm! '
| Parallelogramm | Grundseite g | Höhe h | Flächeninhalt F |
|---|---|---|---|
| A | 3 cm | 2cm | 6 cm² |
| B | 3 cm | 3cm | 9 cm² |
| C | 4 cm | 4,5cm | 18cm² |
| D | 5 | 4cm | 20cm² |
Übung 3 für Profis: Wie ändert sich der Flächeninhalt?
|
Wie verändert sich der Flächeninhalt, im Parallelogramm, wenn... 0-1 Punkt: Kopf hoch! Bearbeite die Aufgabe noch einmal genauer. |
- Du bist wirklich sehr fleißig und hast alle Aufgaben bearbeitet. Sehr gut!
- Du bist wirklich sehr fleißig und hast alle Aufgaben bearbeitet. Sehr gut!
Auf der nächsten Seite findest Du weitere Herleitungsideen für den Flächeninhalt des Parallelogramms. Du kannst sie sicher nachvollziehen, oder?