Vertiefen und Erweitern zum Parallelogramm: Unterschied zwischen den Versionen
(Aufgabe zur Scherung geändert) |
K (→Übung zum Vertiefen) |
||
| Zeile 101: | Zeile 101: | ||
[[Bild:Ebert_Wege.jpg|center]] | [[Bild:Ebert_Wege.jpg|center]] | ||
| − | *'''''Die | + | *'''''Die Straße ist <span style="color: purple">10 Meter</span> vom Haus entfernt. Es sollen neue <span style="color: orange">3 Wege</span> angelegt werden.''''' |
| − | *'''''Die Wege sind 2 Meter breit.''''' | + | *'''''Die Wege sind <span style="color: blue">2 Meter breit</span>.''''' |
| Zeile 113: | Zeile 113: | ||
*'''Brauchst Du wirklich die erste Hilfe dazu?''' | *'''Brauchst Du wirklich die erste Hilfe dazu?''' | ||
{{versteckt| | {{versteckt| | ||
| − | + | Der Weg hat die Form eines Parallelogramms.<br> | |
| − | Länge Grundseite Weg | + | Länge Grundseite Weg 1: 2m <br> |
| − | Länge Höhe Weg | + | Länge Höhe Weg 1: 10m |
}} | }} | ||
<br> | <br> | ||
| Zeile 135: | Zeile 135: | ||
[[Bild:Ebert_Maja.jpg|200px]] | [[Bild:Ebert_Maja.jpg|200px]] | ||
---- | ---- | ||
| + | |||
===Get more and explore=== | ===Get more and explore=== | ||
[[Bild:Ebert_Lob2.jpg|center]] | [[Bild:Ebert_Lob2.jpg|center]] | ||
Version vom 25. Juli 2009, 19:54 Uhr
Variante zur Herleitung
- Du hast bereits eine Möglichkeit gesehn, wie man die Flächeninhaltsformel herleiten kann. Dies ist natürlich nicht die einzige Idee.
| Aufgabenstellung:
1. Verschiebe das dunkel-grüne Dreieck
Das verschobene Dreieck musst du wieder verbergen 2. Erkläre, welche Idee hinter dieser Zerlegung des Parallelogramms steckt.
Zeige dafür wieder die Höhe an.
In diesem Beispiel werden nicht die Parallelogrammseiten betrachtet, die auf den Parallelen Geraden liegen, sondern das andere Seitenpaar. Entsprechend wird die dazugehörige Höhe zur Flächenberechnung gewählt!
|
Nils will dazu noch etwas sagen:
 |
Zur Berechnung der Flächeninhaltsformel kann jede Seite des Parallelogrammes als Grundseite und die zugehörige Höhe genommen werden. |
Flächeninhaltsgleiche Parallelogramme
'Erinnerst Du Dich noch??
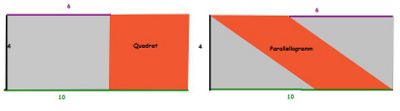
Du hast bereits im ersten Lernpfad nachgewiesen, dass das Parallelogramm und das Quadrat den gleichen Flächeninhalt besitzen. Wie kann man das ohne Ergänzungsgleichheit zeigen???
|
Warum besitzt das blaue Parallelogramm den gleichen Flächeninhalt wie das rote Rechteck ?
Du kannst auch die Höhe anzeigen lassen.
Der Flächeninhalt des Rechtecks beträgt: 12 (cm²) Verändere Parallelogramm mit dem Schieberegler : | |
Das Parallelogramm hat den gleichen Flächeninhalt wie das rote Rechteck,
|
Übung zum Vertiefen
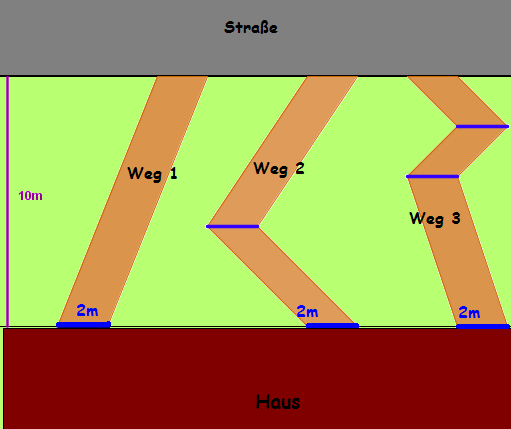
- Die Straße ist 10 Meter vom Haus entfernt. Es sollen neue 3 Wege angelegt werden.
- Die Wege sind 2 Meter breit.
- Ermittle den Flächeninhalt der drei Wege 1,2, und 3
- Berechne zunächst die Fläche des Weg 1.
- Brauchst Du wirklich die erste Hilfe dazu?
Der Weg hat die Form eines Parallelogramms.
Länge Grundseite Weg 1: 2m
Länge Höhe Weg 1: 10m
Die Fläche des Weg 1 beträgt 20(Zahl eintragen)m²
- Nun kannst Du bestimmt die beiden anderen Wege berechnen, oder?
- Brauchst Du ganz sicher auch den nächsten Hinweis?
Der Flächeninhalt von Weg 2 beträgt 20(Zahl eintragen)m²
Der Flächeninhalt von Weg 3 beträgt 20(Zahl eintragen)m²
Get more and explore
Herzlichen Glückwunsch! Du hast nun auch schon den 2. Lernpfad erfolgreich bearbeitet und bist schon ein Profi in der Berechnung von Parallelogrammflächen.
Du wirst im 3. Lernpfad sehen, dass auch andere Figurenflächen sich sehr leicht berechnen lassen.
→Hier gehts weiter zum 3. Lernpfad
Hier geht es zurück zur Seite Übung zum Flächeninhalt Parallelogramm
