Zusammenfassung zur Zerlegungsgleichheit: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K (→Anwendung der Zerlegungsgleichheit: Bild mit Beschreibungen) |
(applet geändert (mehr Dreiecke)) |
||
| Zeile 44: | Zeile 44: | ||
{| | {| | ||
| − | |<ggb_applet height="420" width="650" showResetIcon="true" filename=" | + | |<ggb_applet height="420" width="650" showResetIcon="true" filename="Ebert_PrinzipErgänzung.ggb" /> || |
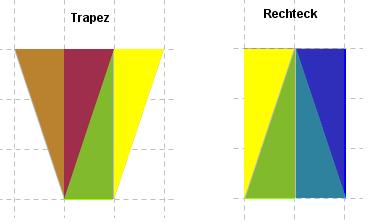
*'''''Zeige, dass das Rechteck und das Trapez zerlegungsgleich sind'''''<br> | *'''''Zeige, dass das Rechteck und das Trapez zerlegungsgleich sind'''''<br> | ||
Du brauchst doch sicher nicht den Lösungshinweis, oder?<br> | Du brauchst doch sicher nicht den Lösungshinweis, oder?<br> | ||
Version vom 29. Juli 2009, 13:42 Uhr
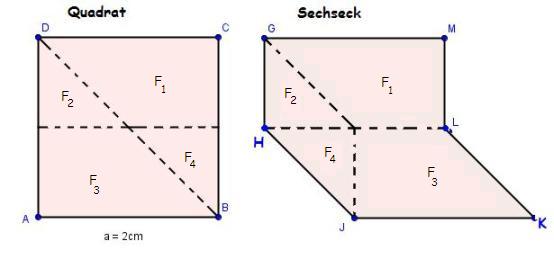
- Übertrage folgende Definition in Dein Heft:
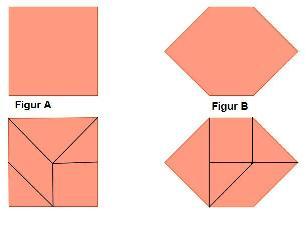
Anwendung der Zerlegungsgleichheit
- Maja weiß jetzt, wozu man die Zerlegungsgleichheit von Figuren nutzen kann. Lies, was sie Dir erzählen möchte:
Ergänzungsgleichheit von Figuren
|
|
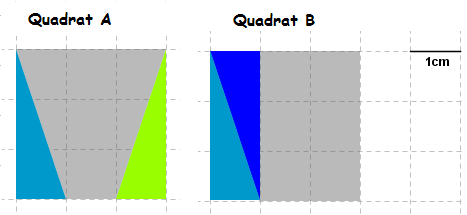
Du brauchst doch sicher nicht den Lösungshinweis, oder?
Vergleiche Deine Lösung hier:
|
|
 |
|
Auf der nächsten Seite kannst Du dein Wissen testen und zeigen, was Du gelernt hast:
→Übung zur Zerlegungsgleichheit
'Hier geht es zurück zur 'Zerlegungsgleichheit von Figuren