Übung zur Zerlegungsgleichheit: Unterschied zwischen den Versionen

Version vom 30. Juli 2009, 17:35 Uhr

Aufgabe 1 zum Aufwärmen

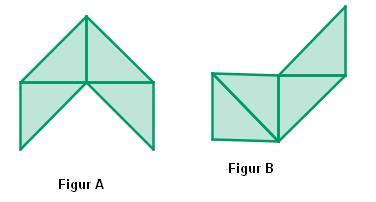
Begründe, warum die folgenden Figuren A und B den gleichen Flächeninhalt besitzen:

Hier siehst Du Majas Lösung. Ist sie richtig? [Anzeigen][Verstecken]

Aufgabe 2 für Geübte: Ergänzungsgleiche Figuren

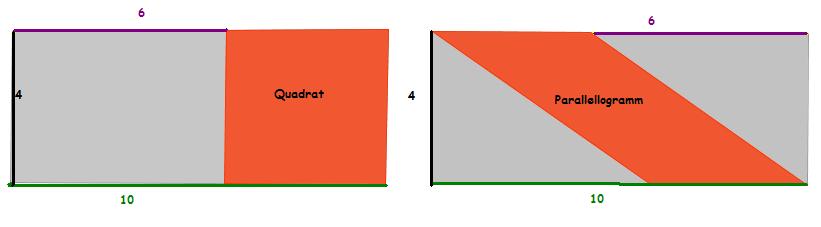
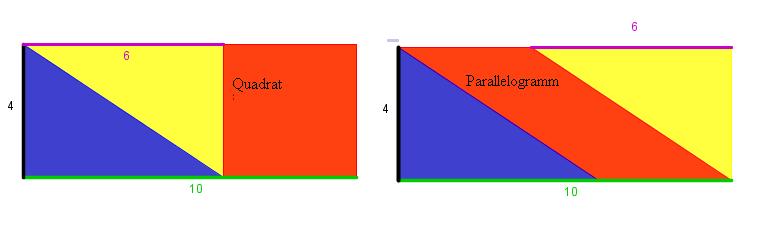
Zwei Rechtecken mit der Länge 10cm und der Breite 4cm ist ein Quadrat und ein Parallelogramm einbeschrieben.

Was haben Quadrat und Parallelogramm gemeinsam?

Tipp:[Anzeigen][Verstecken]

Beantworte dazu die Fragen:

Bist Du ganz sicher, dass Du den Hinweis von Nils brauchst?

[Anzeigen][Verstecken]

Aufgabe 3 für Profis: Wunderliche Parallelogramme

• [BD] ist die Diagonale.
• [FK] eine Parallele zur Seite [DC] und [LM] eine Parallele zu [AD]
• Sie schneiden sich im Punkt S

" Die Parallelogramme SLAF und MCKS besitzen den gleichen Flächeninhalt!"

	Hat Nils Recht? Du kannst S variieren. Beobachte, wie sich Teilfiguren ändern. Die Diagonale (hlrbtaei) das Parallelogramm ABCD. 1. Welche Dreiecke sind kongruent zueinander? Dreieck BDC und Dreieck BAD Dreieck SKB und Dreieck BAD Dreieck DMS und Dreieck SBL Dreieck DMS und Dreieck DSF Dreieck SKB und Dreieck SBL Punkte: 0 / 0
Dreieck DMS und                     sind kongruent zueinander. Ebenso Dreieck                     und SBL. Entfernt man diese Dreiecke von den kongruenten Dreiecken BAD und BDC, so haben die Restfiguren                     und SMCK den gleichen Flächeninhalt. SKBDFSSLAF 1. Die Parallelogramme SLAF und SMCK besitzen den gleichen Flächeninhalt ja nein Punkte: 0 / 0

Get more and explore:

Gratuliere, Du hast den 1. Lernpfad erfolgreich bearbeitet!
Du kennst Dich jetzt schon sehr gut mit zerlegungsgleichen Figuren aus und bist fit die Flächeninhaltsformel von Figuren zu entdecken.

Nils und Maja begleiten dich dabei wieder:

→Hier geht es weiter zum 2. Lernpfad

Hier geht es zurück zur Zusammenfassung zur Zerlegungsgleichheit