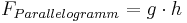Die Flächeninhaltsformel des Parallelogramms: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K (Link eingefügt) |
K (Lückentext verändert) |
||
| Zeile 12: | Zeile 12: | ||
|[[Bild:Ebert_MotivatorHinweis.jpg|200px]] || [[Bild:Ebert_MerkbildParallelogrammneu.jpg|center]] | |[[Bild:Ebert_MotivatorHinweis.jpg|200px]] || [[Bild:Ebert_MerkbildParallelogrammneu.jpg|center]] | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
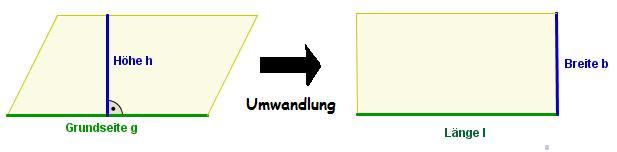
| − | *Länge | + | *Länge l ( im '''Rechteck''') entspricht der '''Grundseite g'''( des Parallelogramms)<br> |
| − | Breite b (Rechteck) | + | Breite b ( im Rechteck) entspricht der '''Höhe h '''( des Parallelogramms)<br> |
*Der Flächeninhalt des Parallelogramms ist definiert als: <br> | *Der Flächeninhalt des Parallelogramms ist definiert als: <br> | ||
F<sub>Parallelogramm</sub> = '''g''' <math>\cdot </math> h mit <br> | F<sub>Parallelogramm</sub> = '''g''' <math>\cdot </math> h mit <br> | ||
Version vom 3. August 2009, 10:07 Uhr
- Jetzt besitzt Du alle Grundlagen, um die Formel für die Berechnung des Flächeninhalts zu erarbeiten.
- Fülle zunächst die Lücken aus und übertrage anschließend den Merkkasten in Dein Heft!
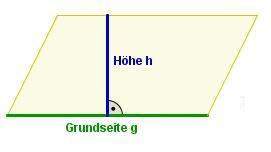
- Erinnerst Du Dich noch an die Herleitungsidee?
 |
Breite b ( im Rechteck) entspricht der Höhe h ( des Parallelogramms)
FParallelogramm = g |
h mit
Zusammenfassung:Flächeninhaltsformel Parallelogramm
- Merke Dir sehr gut, wie man den Flächeninhalt von Parallelogrammen berechnet. Du wirst später darüber abgefragt!
 |
Den Flächeninhalt eines Parallelogramms berechnet man durch: g ist die Länge der Grundseite und h die Länge der dazugehörigen Höhe.  |
Du hast den ersten Lernpfad bald geschafft!
Nur noch ein paar Übungen.
Hier kannst Du Dein wissen testen!!
→Übung zum Flächeninhalt Parallelogramm
Hier geht es zurück zur Seite Höhen im Parallelogramm
