4.Station: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
K
K
Zeile 82: Zeile 82:
 
<br>  
 
<br>  
 
<br>
 
<br>
−
<div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/5.Station|<math>\Rightarrow</math> Weiter zur 5. Station]]</div>
+
<div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/5.Station|<math>\Rightarrow</math> Weiter zur 5. Station: Kreistreue]]</div>
 
<br>
 
<br>
−
<div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/3.Station|<math>\Leftarrow</math> Zurück zur 3. Station]]</div>
+
<div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/3.Station|<math>\Leftarrow</math> Zurück zur 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue]]</div>

Version vom 7. August 2009, 10:24 Uhr

1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung


4. Station: Längenverhältnistreue

Porzelt lobenderDia3.jpg

Porzelt Panto-2.jpg

Längenverhältnistreue liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist.



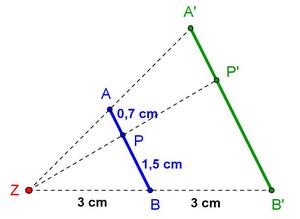Porzelt Verhältnistreu.jpg Arbeitsauftrag:

1.Berechne den Streckungsfaktor k.
2.Berechne \overline{A'P'} und \overline{P'B'}.

3.Berechne {\overline{AP}\over\overline{PB}} und {\overline{A'P'}\over\overline{P'B'}}. Runde auf 2 Nachkommastellen.


Mit Hilfe der folgenden Lückentexte kannst du den Arbeitsauftrag lösen.
Denk konzentriert nach und setze die richtige Aussage in die passende Lücke ein, um die Ergebnisse berechnen zu können:

Lösung zu 1:
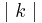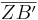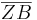
\mid k \mid = \overline{ZB'} : \overline{ZB}
Einsetzen der Werte:
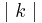\mid k \mid = 6 : 3 = 2 (Berechne das Ergebnis mit dem Taschenrechner)

Porzelt Verhältnistreu.jpg

Lösung zu 2:
\overline{A'P'} = \mid k \mid \cdot \overline{AP}
Einsetzen der Werte:
\overline{A'P'} = 2 \cdot 0,7 cm = 1,4 cm (Berechne das Ergebnis mit dem Taschenrechner)

\overline{P'B'} = \mid k \mid \cdot \overline{PB}
Einsetzen der Werte:
\overline{P'B'} = 2 \cdot 1,5 cm = 3 cm (Berechne das Ergebnis mit dem Taschenrechner)

Lösung zu 3:
Einsetzen der Werte:
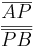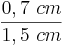{\overline{AP}\over\overline{PB}} = {0,7\ cm \over 1,5\ cm} = 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
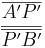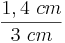{\overline{A'P'}\over\overline{P'B'}} = {1,4\ cm \over 3\ cm} = 0,47 (Berechne das Ergebnis mit dem Taschenrechner)

 


Porzelt lobenderPanto6.jpg

Porzelt fragenderDia-1.jpg


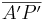Warum ist {\overline{AP}\over\overline{PB}} = {\overline{A'P'}\over\overline{P'B'}}?


Für \overline{A'P'} kann man auch 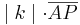\mid k\mid \cdot \overline{AP} und für 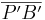\overline{P'B'} kann man 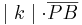\mid k\mid \cdot \overline{PB} einsetzen.
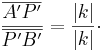
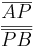Daraus folgt: {\overline{A'P'}\over\overline{P'B'}} ={{|k|}\over{|k|}}\cdot {\overline{AP}\over\overline{PB}}.
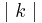\mid k\mid kann man rauskürzen, so dass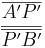 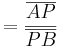{\overline{A'P'}\over\overline{P'B'}} = {\overline{AP}\over\overline{PB}} gilt.

 


Porzelt lobenderDia5.jpg

Ist die zentrische Streckung längenverhältnistreu? (Ja) (!Nein)



\Rightarrow Weiter zur 5. Station: Kreistreue


\Leftarrow Zurück zur 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Zentrische_Streckung/Eigenschaften_der_zentrischen_Streckung/4.Station&oldid=4240“