Litfaßsäule 2: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 112: | Zeile 112: | ||
<br> | <br> | ||
<br> | <br> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
<br> | <br> | ||
| + | <div align="left">[[ Benutzer:Dorothea Rauscher/verschiedene Körper|<math>\Rightarrow</math> Weiter zur nächsten Aufgabe]]</div> | ||
| + | |||
<br> | <br> | ||
Version vom 26. September 2009, 12:51 Uhr
Eine Litfaßsäule besteht aus einem Zylinder mit einem Grundkreisradius von 1,00 m und einer Höhe von 2,00 m. Das Dach hat eine Höhe von 1,00 m und besteht aus einem Kegel.
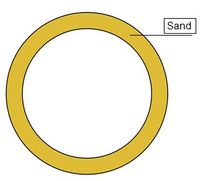
Beim Bau einer Litfaßsäule werden zwei Zylinder ineinandergestellt.
Die Lücke zwischen den zwei Zylindern ist mit Sand gefüllt, um eine gute Stabilität zu gewährleisten.
Je höher die Litfaßsäule ist, desto mehr Sand muss zwischen die beiden Zylinder gefüllt werden, d.h. der Zwischenraum muss größer werden.
Die Mantelfläche des inneren Zylinders hat eine Fläche von 10,68 m2.
(Runde auf zwei Dezimalstellen.)
a. Berechne das Volumen des Zwischenraums.
Das Volumen des äußeren Zylinders beträgt 6,28 m3.
Der Radius des inneren Zylinders ist 0,85 m.
Das Volumen des inneren Zylinders beträgt 4,54 m3.
Somit hat der Zwischenraum ein Volumen von 1,74 m3.
b. Berechne auch, wie viel Sand zum Befüllen des Zwischenraums benötigt wird!
(Dichte von Sand: 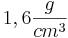 oder
oder 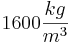 .)
.)
Rechne in 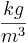 .
.
Zum Befüllen des Zwischenraumes sind 2784 kg Sand notwendig.
c. Wie viel Sand braucht man, wenn sich die Werbefläche (Mantelfläche) um 25% vergrößert, der innere Zylinder aber gleich bleibt?
Die Werbefäche ist statt 12,57 m2 (Alte Größe) jetzt 15,71 m2 groß.
Der neue Radius des äußeren Zylinders ist 1,25 m lang.
Somit beträgt das neue Volumen 9,82 m3 und der Zwischenraum hat ein Volumen von 5,28 m3.
Daraus ergibt sich, dass sich die benötigte Menge Sand auf 8448 kg vergrößert.

 Weiter zur nächsten Aufgabe
Weiter zur nächsten Aufgabe
