Lösungsvorschlag iv): Unterschied zwischen den Versionen

Version vom 28. September 2009, 01:11 Uhr

Lösungsweg:

Die Möglichkeiten, dass das rote Gummibärchen gezogen wird, sind im folgenden Baumdiagramm dargestellt:

Berechnung der Wahrscheinlichkeit:

P(E₄) = P({grün;grün;rot}) + P({grün;gelb;rot}) + P({grün;rot;grün}) + P({grün;rot;gelb}) + P({gelb;grün;rot}) + P({gelb;gelb;rot}) + P({gelb;rot;grün}) + P({gelb;rot;gelb}) +

+ P({rot;grün;grün}) + P({rot;grün;gelb}) + P({rot;gelb;grün}) + P({rot;gelb;gelb}) =

= $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{2}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{2}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{1}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ +

+ $\frac{1}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{2}{3}$ + $\frac{1}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{2}{3}$ + $\frac{1}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ = $\frac{3}{5}$ = 60%

$\Leftarrow$ Zurück

@@ Zeile 1: / Zeile 1: @@
+<big>Lösungsweg:</big>
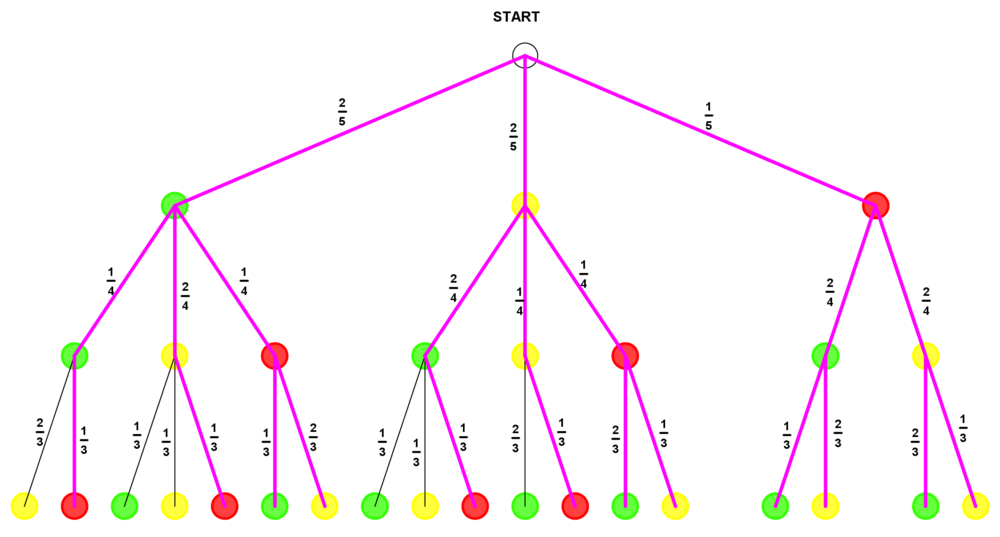
+Die Möglichkeiten, dass das rote Gummibärchen gezogen wird, sind im folgenden Baumdiagramm dargestellt:
+[[Bild:Gummibärchendiagramm4.png|1000px]]
+Berechnung der Wahrscheinlichkeit:
+P(E<sub>4</sub>) = P({grün;grün;rot}) + P({grün;gelb;rot}) + P({grün;rot;grün}) + P({grün;rot;gelb}) + P({gelb;grün;rot}) + P({gelb;gelb;rot}) + P({gelb;rot;grün}) + P({gelb;rot;gelb}) +
++ P({rot;grün;grün}) + P({rot;grün;gelb}) + P({rot;gelb;grün}) + P({rot;gelb;gelb})  =
+= <math>\frac{2}{5}</math> <math>\cdot</math> <math>\frac{1}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> + <math>\frac{2}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> + <math>\frac{2}{5}</math> <math>\cdot</math> <math>\frac{1}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> + <math>\frac{2}{5}</math> <math>\cdot</math> <math>\frac{1}{4}</math> <math>\cdot</math> <math>\frac{2}{3}</math> + <math>\frac{2}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> + <math>\frac{2}{5}</math> <math>\cdot</math> <math>\frac{1}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> + <math>\frac{2}{5}</math> <math>\cdot</math> <math>\frac{1}{4}</math> <math>\cdot</math> <math>\frac{2}{3}</math> + <math>\frac{2}{5}</math> <math>\cdot</math> <math>\frac{1}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> + <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> +
++ <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{2}{3}</math> + <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{2}{3}</math> + <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> = <math>\frac{3}{5}</math> = 60%
 <div align="left">[[Zusammengesetzte Zufallsexperimente und Pfadregeln|<math>\Leftarrow</math> Zurück]]</div>

Lösungsvorschlag iv): Unterschied zwischen den Versionen

Version vom 28. September 2009, 01:11 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge