Lösungsvorschlag iv)
Aus DMUW-Wiki
möglicher Lösungsweg:
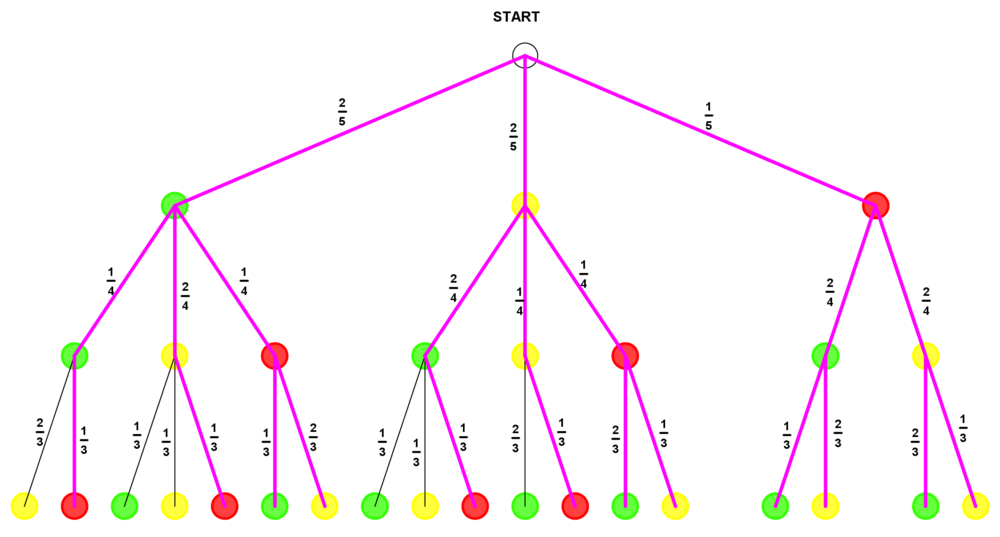
Die Möglichkeiten, dass das rote Gummibärchen gezogen wird, sind im folgenden Baumdiagramm dargestellt:
Berechnung der Wahrscheinlichkeit:
P(E4) = P({grün;grün;rot}) + P({grün;gelb;rot}) + P({grün;rot;grün}) + P({grün;rot;gelb}) + P({gelb;grün;rot}) + P({gelb;gelb;rot}) + P({gelb;rot;grün}) + P({gelb;rot;gelb}) +
+ P({rot;grün;grün}) + P({rot;grün;gelb}) + P({rot;gelb;grün}) + P({rot;gelb;gelb}) =
= 



 +
+ 



 +
+ 



 +
+ 



 +
+ 



 +
+ 



 +
+ 



 +
+ 



 +
+ 



 +
+
+ 



 +
+ 



 +
+ 



 =
=  = 60%
= 60%
 Zurück
Zurück
