Zusammengesetzte Zufallsexperimente und Pfadregeln: Unterschied zwischen den Versionen
K (→Aufgabe 3:) |
K |
||
| Zeile 1: | Zeile 1: | ||
| − | == Aufgabe 1: == | + | == Aufgabe 1: == |
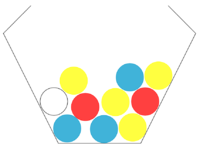
| − | :: | + | :: In einer Urne befinden sich zehn Kugeln: vier gelbe, drei blaue, zwei rote und eine weiße. [[Bild:UrneAufgabe3.png|200px]] |
| − | :: | + | :: Es werden nun nacheinander zwei Kugeln gezogen. Nach jedem Zug werden die Kugeln zurück in die Urne gelegt. |
| − | :: | + | :: Die Farben werden im Folgenden abgekürzt: g = gelb, b = blau, r = rot, w = weiß |
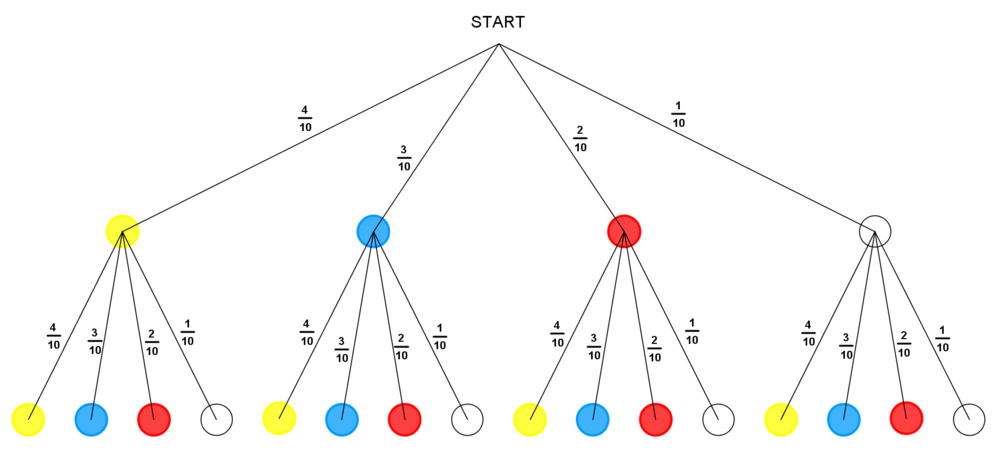
| − | :: | + | :: Hier wird das dazugehörige Baumdiagramm gezeigt: |
| − | : | + | [[Bild:BaumAufgabe3.png|1000px|center]] |
| − | + | :: Ordne nun den verschiedenen Wahrscheinlichkeiten ihre Werte zu und umgekehrt. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | :: | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div class="zuordnungs-quiz"> | ||
| + | {| | ||
| + | |- | ||
| + | | P({g;g}) || 16% | ||
| + | |- | ||
| + | | P({w;w}) || 1% | ||
| + | |- | ||
| + | | P({r;w}) || 2% | ||
| + | |- | ||
| + | | P({b;g}) || 12% | ||
| + | |- | ||
| + | | P({r;b}) || 6% | ||
| + | |- | ||
| + | | P({g;w}) || 4% | ||
| + | |- | ||
| + | | P({b;w}) || 3% | ||
| + | |- | ||
| + | | P({r;g}) || 8% | ||
| + | |- | ||
| + | | P({b;b}) || 9% | ||
| + | |} | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 178: | Zeile 124: | ||
| − | == Aufgabe 3: == | + | == Aufgabe 3: == |
| − | :: | + | :: Es wird zunächst ein klassischen Würfel und im Anschluss eine Münze geworfen. |
| − | :: | + | :: a) Wie sieht das dazugehörige Baumdiagramm aus? |
| − | :: | + | :: Zeichne es in dein Heft und vergleiche anschließend mit der Lösung hier |
| − | :: | + | :: [[Baumdiagramm Würfel und Münzwurf]] |
| − | + | :: b) Kreuze alle Elemente an, die zum Ergebnisraum gehören: | |
| − | :: | + | <div class="multiplechoice-quiz"> |
| + | |||
| + | ({1;W}) ({1;Z}) ({2;W}) ({2;Z}) ({3;W}) ({3;Z}) ({4;W}) ({4;Z}) ({5;W}) ({5;Z}) ({6;W}) ({6;Z}) (!{1;1}) (!{2;3}) (!{4;2}) (!{5;1}) (!{W;Z}) (!{Z;W}) (!{0;W}) (!{W;1}) (!{Z;5}) (!{W;2}) (!{2;6}) (!{6;6}) | ||
| + | |||
| + | </div> | ||
| + | |||
| + | :: c) Vervollständige dein Baumdiagramm aus Teilaufgabe a), indem du die einzelnen Wahrscheinlichkeiten an jeden Pfad schreibst. | ||
| + | :: Kontrollieren kannst du das Ergebnis mithilfe des folgenden Links: | ||
| + | |||
| + | :: [[Baumdiagramm mit den Wahrscheinlichkeiten]] | ||
| + | |||
| + | :: d) Berechne mithilfe der Pfadregeln die Wahrscheinlichkeiten der Ereignisse: | ||
| + | |||
| + | ::: i) E<sub>1</sub>: Es wird eine 1 gewürfelt: | ||
| + | |||
| + | ::: Markiere im Baumdiagramm die zugehörigen Pfade gelb. | ||
| + | ::: Kreuze die richtige Antwort an: | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | P(E<sub>1</sub>) ist (!<math>\frac{1}{12}</math>) (<math>\frac{1}{6}</math>) (!25%) (!<math>\frac{2}{3}</math>) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
| + | |||
| + | Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren: | ||
| + | |||
| + | [[Kontrolle i)]] | ||
| + | |||
| + | |||
| + | ::: ii) E<sub>2</sub>: Es wird Zahl geworfen | ||
| + | |||
| + | ::: Markiere im Baumdiagramm die zugehörigen Pfade grün | ||
| + | |||
| + | ::: Kreuze die richtige Antwort an: | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | P(E<sub>2</sub>) ist (!<math>\frac{1}{6}</math>) (!<math>\frac{1}{12}</math>) (!<math>\frac{1}{3}</math>) (50%) | ||
| + | |||
| + | </div> | ||
| + | |||
| + | Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren: | ||
| + | |||
| + | [[Kontrolle ii)]] | ||
| + | |||
| + | |||
| + | ::: iii) E<sub>3</sub>: Es wird eine ungerade Augenzahl gewürfelt | ||
| + | |||
| + | ::: Markiere im Baumdiagramm die zugehörigen Pfade blau | ||
| + | |||
| + | ::: Kreuze die richtige Antwort an: | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | P(E<sub>3</sub>) ist (<math>\frac{1}{2}</math>) (!35%) (!<math>\frac{1}{6}</math>) (!<math>\frac{3}{4}</math>) | ||
| + | |||
| + | </div> | ||
| + | |||
| + | Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren: | ||
| + | |||
| + | [[Kontrolle iii)]] | ||
| + | |||
| + | |||
| + | ::: iv) E<sub>4</sub>: Es wird mindestens eine 5 gewürfelt | ||
| + | |||
| + | ::: Markiere im Baumdiagramm die zugehörigen Pfade rot | ||
| + | |||
| + | ::: Kreuze die richtige Anwort an: | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | P(E<sub>4</sub>) ist (!30%) (<math>\frac{1}{3}</math>) (!<math>\frac{1}{4}</math>) (!<math>\frac{1}{6}</math>) | ||
| + | |||
| + | </div> | ||
| + | |||
| + | Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren: | ||
| + | |||
| + | [[Kontrolle iv)]] | ||
| + | |||
== Aufgabe 4: == | == Aufgabe 4: == | ||
Version vom 28. September 2009, 03:54 Uhr
Inhaltsverzeichnis |
Aufgabe 1:
- Es werden nun nacheinander zwei Kugeln gezogen. Nach jedem Zug werden die Kugeln zurück in die Urne gelegt.
- Die Farben werden im Folgenden abgekürzt: g = gelb, b = blau, r = rot, w = weiß
- Hier wird das dazugehörige Baumdiagramm gezeigt:
- Ordne nun den verschiedenen Wahrscheinlichkeiten ihre Werte zu und umgekehrt.
| P({g;g}) | 16% |
| P({w;w}) | 1% |
| P({r;w}) | 2% |
| P({b;g}) | 12% |
| P({r;b}) | 6% |
| P({g;w}) | 4% |
| P({b;w}) | 3% |
| P({r;g}) | 8% |
| P({b;b}) | 9% |
Aufgabe 2:
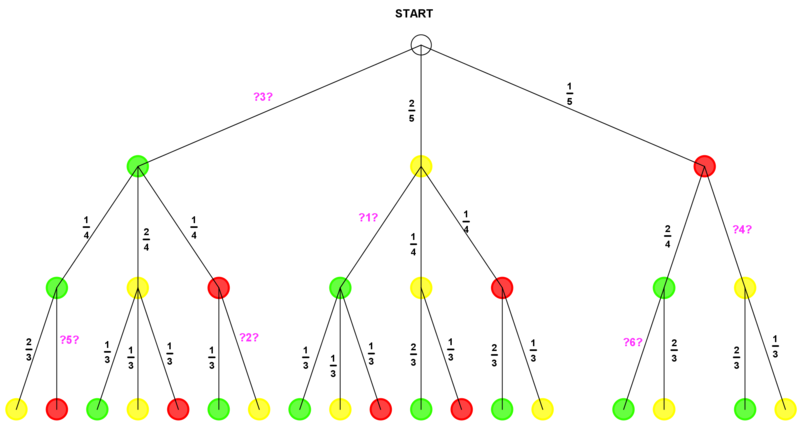
- Du hast 5 Gummibärchen vor dir liegen, 2 grüne, 2 gelbe und 1 rotes. Du ziehst nacheinander drei Gummibärchen, um sie zu essen.
- Das Baumdiagramm zu diesem Zufallsexperiment siehst du hier abgebildet.
- a) In dem Baumdiagramm fehlen allerding einige Wahrscheinlichkeiten.
Die Lücken sind mithilfe von Fragezeichen und Zahlen durch nummeriert von ?1? bis ?6?. - Ordne die fehlenden Wahrscheinlichkeiten den jeweiligen Lücken zu:
- a) In dem Baumdiagramm fehlen allerding einige Wahrscheinlichkeiten.
| ?1? | 
|
| ?2? | 
|
| ?3? | 
|
| ?4? | 
|
| ?5? | 
|
| ?6? | 
|
- b) Berechne die Wahrscheinlichkeit für folgende Ereignisse:
- i) E1: Es werden 2 grüne Gummibärchen hintereinander gezogen
Antwort: Die Wahrscheinlichkeit, dass 2 grüne Gummibärchen hintereinander gezogen werden, beträgt 20% (Das Ergebnis bitte in Prozent angeben, also beispielsweise 50%)
- ii) E2: Es wird von jeder Farbe ein Gummibärchen gezogen
Antwort: Die Wahrscheinlichkeit, dass ein Gummibärchen jeder Farbe gezogen wird, beträgt 40% (Das Ergebnis bitte in Prozent angeben, also beispielsweise 50%)
- iii) E3: Es wird höchstens ein gelbes Gummibärchen gezogen
Antwort: Die Wahrscheinlichkeit, dass höchstens ein gelbes Gummibärchen gezogen wird, beträgt 70% (Das Ergebnis bitte in Prozent angeben, also beispielsweise 50%)
- iv) E4: Es wird das rote Gummibärchen gezogen
Antwort: Die Wahrscheinlichkeit, dass das rote Gummibärchen gezogen wird, beträgt 60% (Das Ergebnis bitte in Prozent angeben, also beispielsweise 50%)
- v) E5: Es wird kein grünes Gummibärchen gezogen
Antwort: Die Wahrscheinlichkeit, dass kein grünes Gummibärchen gezogen wird, beträgt 10% (Das Ergebnis bitte in Prozent angeben, also beispielsweise 50%)
Aufgabe 3:
- Es wird zunächst ein klassischen Würfel und im Anschluss eine Münze geworfen.
- a) Wie sieht das dazugehörige Baumdiagramm aus?
- Zeichne es in dein Heft und vergleiche anschließend mit der Lösung hier
- b) Kreuze alle Elemente an, die zum Ergebnisraum gehören:
({1;W}) ({1;Z}) ({2;W}) ({2;Z}) ({3;W}) ({3;Z}) ({4;W}) ({4;Z}) ({5;W}) ({5;Z}) ({6;W}) ({6;Z}) (!{1;1}) (!{2;3}) (!{4;2}) (!{5;1}) (!{W;Z}) (!{Z;W}) (!{0;W}) (!{W;1}) (!{Z;5}) (!{W;2}) (!{2;6}) (!{6;6})
- c) Vervollständige dein Baumdiagramm aus Teilaufgabe a), indem du die einzelnen Wahrscheinlichkeiten an jeden Pfad schreibst.
- Kontrollieren kannst du das Ergebnis mithilfe des folgenden Links:
- d) Berechne mithilfe der Pfadregeln die Wahrscheinlichkeiten der Ereignisse:
- i) E1: Es wird eine 1 gewürfelt:
- Markiere im Baumdiagramm die zugehörigen Pfade gelb.
- Kreuze die richtige Antwort an:
P(E1) ist (!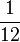 ) (
) ( ) (!25%) (!
) (!25%) (! )
)
Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren:
- ii) E2: Es wird Zahl geworfen
- Markiere im Baumdiagramm die zugehörigen Pfade grün
- Kreuze die richtige Antwort an:
P(E2) ist (! ) (!
) (!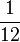 ) (!
) (! ) (50%)
) (50%)
Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren:
- iii) E3: Es wird eine ungerade Augenzahl gewürfelt
- Markiere im Baumdiagramm die zugehörigen Pfade blau
- Kreuze die richtige Antwort an:
P(E3) ist ( ) (!35%) (!
) (!35%) (! ) (!
) (! )
)
Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren:
- iv) E4: Es wird mindestens eine 5 gewürfelt
- Markiere im Baumdiagramm die zugehörigen Pfade rot
- Kreuze die richtige Anwort an:
P(E4) ist (!30%) ( ) (!
) (! ) (!
) (! )
)
Hier kannst du deinen Rechenweg und die Markierung der Pfade kontrollieren:
Aufgabe 4:
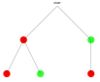
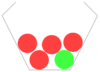
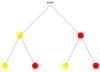
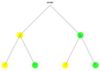
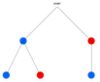
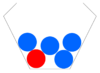
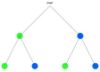
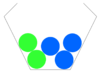
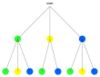
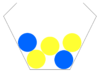
- Finde die zusammengehörenden Baumdiagramme und Urnen.
- In allen dargestellten Zufallsversuchen wird zweimal aus der Urne gezogen, ohne die gezogenen Kugeln zurück zu legen.







 Zurück
Zurück
