zusammengesetzte Körper 2: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K (Fehler 1) |
K (Hinweise geändert) |
||
| Zeile 15: | Zeile 15: | ||
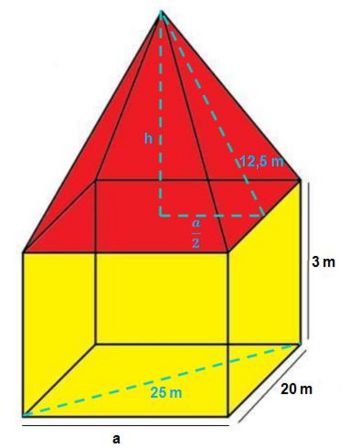
Das Volumen der Pyramide beträgt '''1000 (m<sup>3</sup>)'''. Das Volumen des Quaders '''900 (m<sup>3</sup>)'''. Somit ist das Gesamtvolumen '''1900 (m<sup>3</sup>)''' m<sup>3</sup>. | Das Volumen der Pyramide beträgt '''1000 (m<sup>3</sup>)'''. Das Volumen des Quaders '''900 (m<sup>3</sup>)'''. Somit ist das Gesamtvolumen '''1900 (m<sup>3</sup>)''' m<sup>3</sup>. | ||
</div> | </div> | ||
| − | <popup name="Hinweis"> | + | <popup name="Hinweis"> Was weißt du über die Grundfläche eines Quaders? |
| + | <br> Aus welcher Figur besteht sie?<br> Wie groß sind die Winkel dieser Figur? <br> Du kannst die Grundfläche in zwei Dreiecke zerlegen? <br> Welche spezielle Eigenschaft benötigen die Dreiecke, damit du die Aufgabe lösen kannst? <br> Wie steht die Höhe auf der Grundseite? </popup> | ||
|- style="background-color:#EED5D2 " | |- style="background-color:#EED5D2 " | ||
| Zeile 28: | Zeile 29: | ||
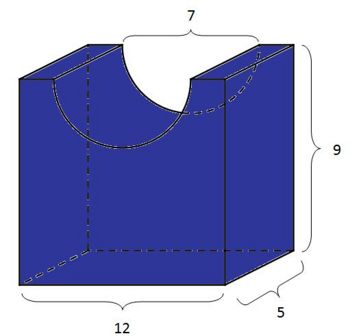
<br> Das Volumen verringert sich um '''18 (%)''' %. | <br> Das Volumen verringert sich um '''18 (%)''' %. | ||
</div> | </div> | ||
| − | <popup name="Hinweis"> | + | <popup name="Hinweis">Erinnere dich was du alles über den Radius weißt. <br> Was für ein Körper wird aus dem Quader herausgeschnitten?</popup> |
|- style="background-color:#EED5D2 " | |- style="background-color:#EED5D2 " | ||
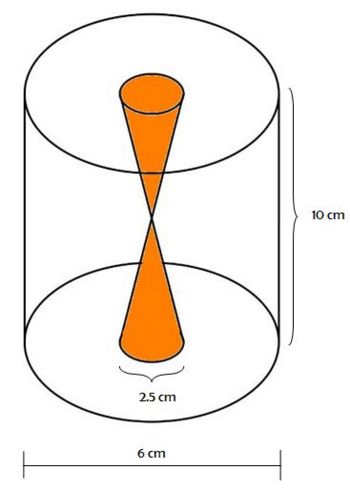
| − | | [[Bild:Kegelino_Dorothea RAuscher_26.09.jpg|350px]] || '''Hinweis: Der Rauminhalt der beiden Kegel ist identisch.'''<br> '''Berechne den Rauminhalt des Zylinders ohne die Kegel.''' <br> ''(Runde auf ganze Zahlen!)'' | + | | [[Bild:Kegelino_Dorothea RAuscher_26.09.jpg|350px]] || '''Hinweis: Der Rauminhalt der beiden Kegel ist identisch.'''<br> '''Berechne den Rauminhalt des Zylinders ohne die beiden Kegel.''' <br> ''(Runde auf ganze Zahlen!)'' |
<br> | <br> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Das Volumen des Zylinders beträgt '''283 (cm<sup>3</sup>)'''. Das Volumen der beiden Kegel beträgt jeweils '''8 (cm<sup>3</sup>)''', zusammen also '''16 (cm<sup>3</sup>)'''. Somit ist das Gesamtvolumen '''267 (cm<sup>3</sup>)''' cm<sup>3</sup>. | Das Volumen des Zylinders beträgt '''283 (cm<sup>3</sup>)'''. Das Volumen der beiden Kegel beträgt jeweils '''8 (cm<sup>3</sup>)''', zusammen also '''16 (cm<sup>3</sup>)'''. Somit ist das Gesamtvolumen '''267 (cm<sup>3</sup>)''' cm<sup>3</sup>. | ||
</div> | </div> | ||
| − | <popup name="Hinweis"> | + | <popup name="Hinweis">Kannst du dich bei der Berechnung des Radius an eine ähnliche Aufgabe erinnern? <br> Beide Kegel sind identisch und passen der Höhe nach genau in den Zylinder. Überlege, wie du die Höhe eines einzelnen Kegels bestimmen kannst.</popup> |
|- style="background-color:#EED5D2 " | |- style="background-color:#EED5D2 " | ||
Aktuelle Version vom 17. November 2009, 11:25 Uhr
zusammengesetzte Körper 2
Bearbeite die Aufgaben!
BEACHTE: Dir steht auch die Formelsammlung zur Verfügung!
 |
Die Seite a ist 15 (m) lang. Die Höhe h der Pyramide beträgt 10 (m).
|
 |
(Runde auf ganze Zahlen)
|
 |
Hinweis: Der Rauminhalt der beiden Kegel ist identisch. Berechne den Rauminhalt des Zylinders ohne die beiden Kegel. (Runde auf ganze Zahlen!)
Das Volumen des Zylinders beträgt 283 (cm3). Das Volumen der beiden Kegel beträgt jeweils 8 (cm3), zusammen also 16 (cm3). Somit ist das Gesamtvolumen 267 (cm3) cm3. |
 |
Das Volumen des Quaders beträgt 400 (m3). Das Volumen des Prismas 48(m3). Somit ist das Gesamtvolumen 352 (m3) m3. |
