Seite 3
2.Station: Multiplikation zweier Brüche
Einführung:
enaktiv-> Schieberegler
Bearbeite nun die folgenden Aufgabe!!! Benutze dabei den Schieberegler!!!
 von
von  = (
= (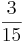 ) (!
) (!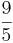 ) (!
) (!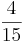 )
)
 von
von  = (
= (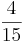 ) (!
) (!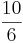 ) (!
) (!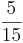 )
)
 von
von  = (
= (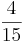 ) (!
) (!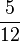 ) (!
) (!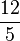 )
)
 von
von  = (
= (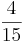 ) (!
) (!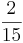 ) (!
) (! )
)
- Veranschaulichung:
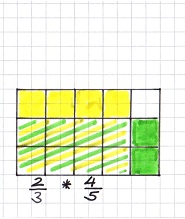
Beispiel von oben:
Anhand der Zeichnung wird die Multiplikation zweier Brüche nochmals veranschaulicht.
Wie du sehen kannst, ist die Multiplikationsaufgabe genau die gelb/grün schraffierte Fläche!
Ebenfalls erkennst du, dass das Wort von mit dem mathematischen Zeichen * übersetzt werden kann!
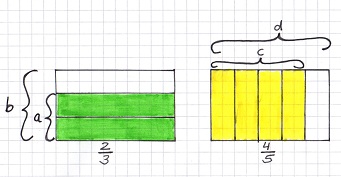
 *
*  =
= 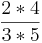 =
= 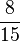 (gelb/grün schraffierte Fläche)
(gelb/grün schraffierte Fläche)
Versuche die Rechenregel für die Multiplikation zweier Brüche zu finden
Lies dir den Text genau durch und schaue dabei auf die nebenstehenden Beispiele. Ziehe die Wörte mit der linken Maustaste in die Platzhalter. Richtige Antworten bleiben stehen, falsche fallen wieder zurück. Wenn du etwas falsch eingefügt hast, probiere es nochmal.
Multiplikation zweier Brüche
 *
* 
1) Multpliziere die Zähler miteinander.
2) Ebenfalls werden die Nenner beider Brüche miteinander multipliziert  *
* =
= 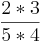
3) Kürze das Ergebnis soweit wie möglich! 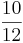 =
= 
4) Wandle den Bruch (wenn möglich) in einen gemischten Bruchum.
- Zusammenfassung:
| Allgemein: |
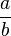 * * 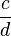 = = 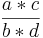
|


