WSW-Satz-1

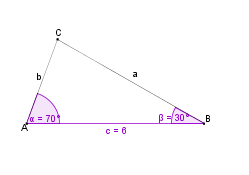
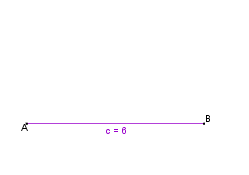
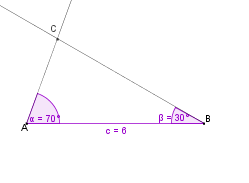
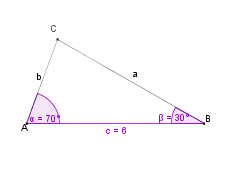
Wie konstruiert man ein Dreieck, von dem die Länge einer Seite und die Maße der beiden anliegenden Winkel gegeben sind?

Wir wollen ein Dreieck konstruieren, von dem die Seite c = 6 cm,
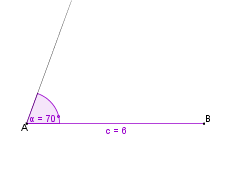
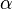
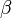
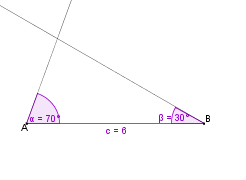
sowie die anliegenden Winkel $\alpha$$=$70° und $\beta$$=$30° gegeben sind.

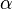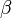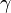
Anmerkung: Es gilt $\alpha$ + $\beta$ + $\gamma$ $=$ 180°. Somit kann das Maß des dritten Winkels berechnet werden.
Deshalb ist die Konstruktion eines Dreiecks, von dem eine Seitenlänge und zwei Innenwinkelmaße gegeben sind, IMMER möglich.

Um das Dreieck zu konstruieren fertigen wir zunächst eine Skizze an. Dazu zeichnen wir ein beliebiges Dreieck und markieren alle gegebenen Größen farbig.
Wir beginnen mit der Grundseite c = 6 cm.
Am Punkt A tragen wir den Winkel $\alpha$$=$70° gegen den Uhrzeigersinn ab.
Am Punkt B tragen wir den Winkel $\beta$$=$30° im Uhrzeigersinn ab. VORSICHT: Klicke zuerst auf den Punkt A, dann auf den Punkt B und gib dann die Winkelgröße an. Vergiss nicht die RICHTUNG des Winkels zu ändern!!
Die Halbgeraden der Winkel schneiden sich im Punkt C.
Somit erhalten ein eindeutig festgelegtes Dreieck.

Merke WSW-Satz Dreiecke sind zueinander kongruent, wenn sie in der Länge von einer Seite und den Maßen der beiden anliegenden Winkel übereinstimmen (Winkel-Seite-Winkel-Satz). oder: Man kann ein Dreieck eindeutig konstruieren wenn die Länge einer Seite und die Maße der beiden anliegenden Winkel gegeben sind.

Aufgabe   Übertrage den Satz auf deinen Laufzettel!

$\Rightarrow$ Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.