Zusammenfassung zur Zerlegungsgleichheit

Übertrage folgende Definition in Dein Heft:

Zerlegungsgleichheit von Figuren Zwei Figuren sind zerlegungsgleich, wenn sie in paarweise kongruente Teilfiguren zerlegt werden können. Beispiel: Figur A und Figur B sind zerlegungsgleich. Zerlegungsgleiche Figuren besitzen den gleichen Flächeninhalt

Anwendung der Zerlegungsgleichheit

Maja weiß jetzt, wozu man die Zerlegungsgleichheit von Figuren nutzen kann. Lies, was sie Dir erzählen möchte:

Ich weiß bereits, wie man den Flächeninhalt von Quadraten berechnet, wenn die Seitenlänge gegeben ist. Die Seitenlänge des Quadrates ist 2 cm. Damit ist der Flächeninhalt 4(cm²) Da das nebenstehende Sechseck zerlegungsgleich zum Quadrat ist und damit den gleichen Flächeninhalt wie das Quadrat besitzt. kennen wir auch den Flächeninhalt des Sechsecks. Man kann die Berechnung des Flächeninhaltes von Figuren, für die man keine Berechnungsformel kennt, auf Figuren zurückführen, für die man eine Flächeninhaltsformel kennt.

---

Ergänzungsgleichheit von Figuren

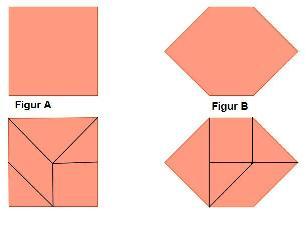
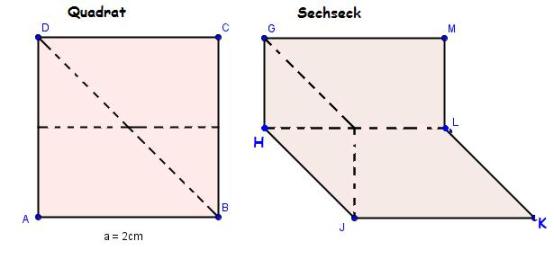
Zeige, dass das Rechteck und das Trapez zerlegungsgleich sind Ergänze das Trapez und das Rechteck jeweils zu einem Quadrat mit Seitenlänge 3cm: Applet

• Die beiden Quadrate sind zerlegungs-gleich

• Wenn man zum Trapez und zum Rechteck jeweils kongruente Figuren (Dreiecke) hinzufügt - also ergänzt, so sind die beiden entstehenden Figuren auch zerlegungsgleich (Bild)

• Das Trapez und das Rechteck nennt man daher auch ergänzungsgleich.

Figuren sind ergänzungsgleich, wenn man sie durch Ergänzung mit der gleichen Zahl kongruenter Figuren in zerlegungsgleiche Figuren umwandeln kann. Ergänzungsgleiche Figuren sind zerlegungsgleich.

Auf der nächsten Seite kannst Du dein Wissen testen und zeigen, was Du gelernt hast:
→Übung zur Zerlegungsgleichheit

'Hier geht es zurück zur 'Zerlegungsgleichheit von Figuren