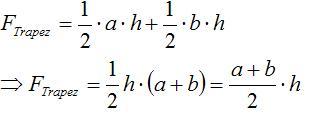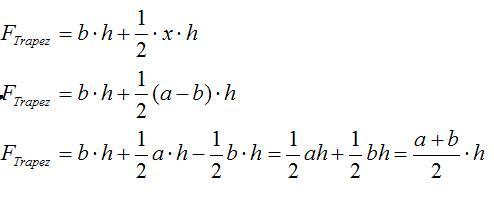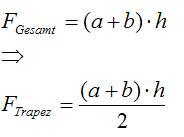Aufgabensammlung zur Flächeninhaltsberechnung
Aus DMUW-Wiki
< Lernpfade | Flächeninhalt ebener Figuren
Version vom 20. Juli 2009, 13:58 Uhr von Michael Schuster (Diskussion | Beiträge)
- Es gibt ein Sprichwort, dass Du sicher kennst: "Übung macht den Meister!"
- Werde zum Meister für Flächenberechnungen!
- Genügend Übungen findest Du hier:
Für absolute Profis gibt es hier noch 3 Aufgaben
Die nächste Aufgabe erfordert etwas Geschick und einen guten Blick!
Schaffst Du es ohne Hinweise?
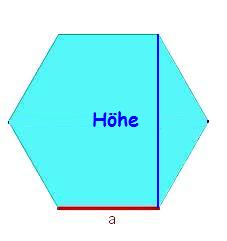
Aufgabe 1 Das Sechseck
- Berechne den Flächeninhalt des gegebenen Sechsecks. Es besitzt die Seitenlänge a = 3 cm . Die Höhe ist
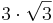 cm hoch.
cm hoch.
- Runde auf die erste Nachkommastelle.
Tipp:
Welche Teilfiguren (Dreieck, Parallelogramm?) könnten sich denn hinter einem Sechseck verbergen??
Hier findest Du einen weiteren Hinweis:
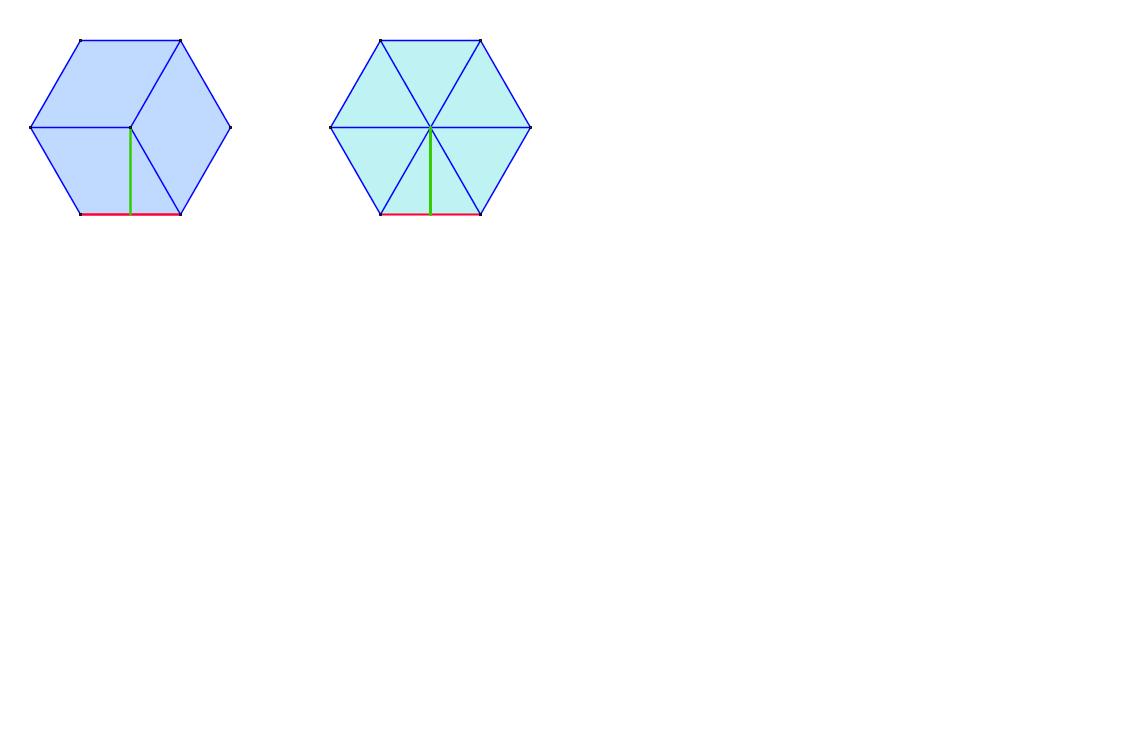
Für die Berechnung des Flächeninhalts eines regelmäßigen Sechsecks kannst Du natürlich mehrere Wege gehen. Hier siehst Du 2 Ansatzmöglichkeiten:
Jetzt kannst Du sicher den Flächeninhalt des Sechsecks berechnen, oder?
Das Sechseck hat einen Flächeninhalt von 23,4 (cm²).
Die nächste Aufgabe knifflig. Wenn Du sie löst bist Du sehr gut!
Aufgabe 2: Umwandlungen
- Gegeben ist ein Dreieck mit folgenden Maßen:
- Länge der Höhe: 9cm
- Länge der dazugehörigen Grundseite: 6cm
Arbeitsauftrag:
Diess Aufgabe ist wirklich für absolute Profis! Zeig was in Dir steckt!
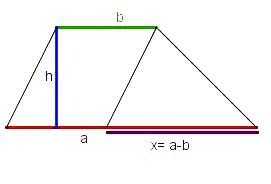
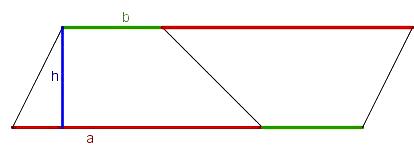
Aufgabe 3. Das Trapez
- Hier siehst Du die Flächeninhaltsformel für das Trapez:
- Es gibt verschiedene Varianten diese Formel herzuleiten. Auch Du kannst mit denen Dir zur Verfügung stehenden Mitteln, die Flächeninhaltsformel herleiten.
- Du siehst hier 3 Bilder mit Lösungsideen zur Trapezberechnung. Dazu gibt es 3 entsprechende Rechenwegen, die die Lösungsidee repräsentieren:
- Arbeitsauftrag:
- 1. Ordne den passenden Rechenweg dem richtigen Bild zu.
- 2.Übernehme eine Lösungsidee mit Bild und Rechenweg in Dein Heft