 So, jetzt vergleichen wir einmal die Konstruktionen und ihre Beschreibungen!
So, jetzt vergleichen wir einmal die Konstruktionen und ihre Beschreibungen!
Konstruktionsbeschreibung zu a) mit a = 7,5 cm, b = 4,5 cm und c = 3,5 cm
| 1. |
Zunächst überprüfen wir mit Hilfe der Dreiecksungleichung, ob das Dreieck konstruierbar ist.
a + b > c, 7,5 cm + 4,5 cm = 12 cm > 3,5 cm
b + c > a, 4,5 cm + 3,5 cm = 8 cm > 7,5 cm
c + a > b, 3,5 cm + 7,5 cm = 11 cm > 4,5 cm.
|
Das Dreieck ist konstruierbar!
|
| 2. |
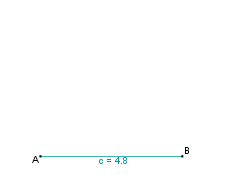
Wir beginnen mit der Grundseite c = 3,5 cm. |
|
| 3. |
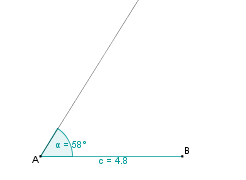
Dann zeichnen wir einen Kreis mit Radius a = 7,5 cm um B. |
|
| 4. |
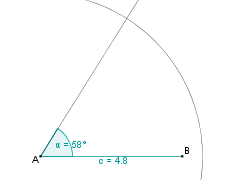
Danach zeichnen wir einen Kreis mit Radius b = 4,5 cm um A. |
|
| 5. |
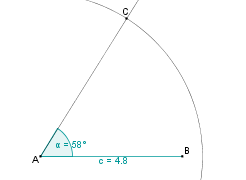
Die beiden Kreise schneiden sich in 2 Punkten. Diese Schnittpunkte nennen wir C1 und C2. |
|
| 6. |
Um ein Dreieck zu erhalten verbinden wir jetzt noch die Punkte A, B und C1, bzw. A, B und C2. |
|
Konstruktionsbeschreibung zu b) mit a = b = 7 cm und c = 4 cm
Konstruktionsbeschreibung zu c) mit a = 3 cm, b = 2 cm und c = 7 cm
| 1. |
Zunächst überprüfen wir mit Hilfe der Dreiecksungleichung, ob das Dreieck konstruierbar ist.
a + b > c, 3 cm + 2 cm = 5 cm < 7 cm
b + c > a, 2 cm + 7 cm = 9 cm > 3 cm
c + a > b, 7 cm + 3 cm = 10 cm > 2 cm
|
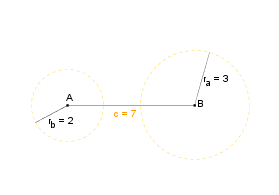
Das Dreieck ist nicht konstruierbar!
|
 |
Super! Du kennst dich ja schon gut aus!
|
 Schauen wir uns einmal den nächsten Satz an!
Schauen wir uns einmal den nächsten Satz an!
 So, jetzt vergleichen wir einmal die Konstruktionen und ihre Beschreibungen!
So, jetzt vergleichen wir einmal die Konstruktionen und ihre Beschreibungen!





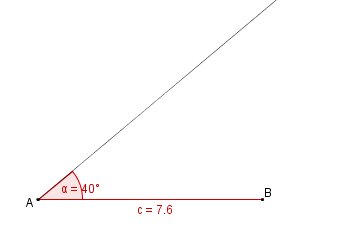
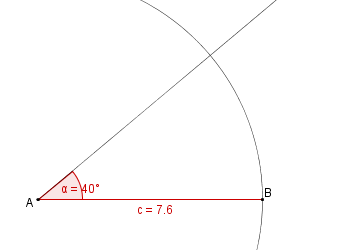
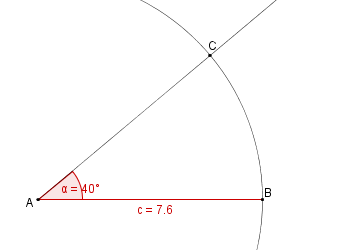
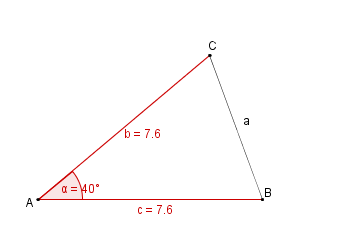

 Schauen wir uns einmal den nächsten Satz an!
Schauen wir uns einmal den nächsten Satz an!
