1. Fußball-WM 2006 - Wasserverbrauch
Quadratische Funktionen
| Auf der rechten Seite ist eine andere quadratische Funktion abgebildet. Ihr Funktionsterm hat die Form x². Wie wir schon festgestellt haben, unterscheiden sich die Graphen quadratischer Funktionen stark von den Graphen linearer Funktionen.
Hier erfährst du alle wichtigen Merkmale der quadratischen Funktion:
|
Merke:
Die Graphen von Funktionen mit der Funktionsgleichung 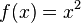 heißen Parabeln. heißen Parabeln.
Sie sind symmetrisch zur y-Achse. Der Punkt 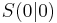 heißt Scheitel der Parabel und ist der tiefste Punkt. heißt Scheitel der Parabel und ist der tiefste Punkt.
|
Schön, nun wissen wir, dass wir es mit Parabeln zu tun haben. Diese sind jedoch nicht immer in der starren Form f(x)=x² dargestellt. In der folgenden Aufgabe kannst du diese Parabel durch einen Schieberegler  verändern.
Aber sieh dir das selbst mal an. verändern.
Aber sieh dir das selbst mal an.
|
|
|
Aufgabe x
|
Bei der Suche nach einer passenden Sprungbahn ist dir sicherlich aufgefallen, dass sich der Name der Funktion geändert hat. Vor dem x² ist plötzlich eine Zahl erschienen. Unsere Funktion erhält also eine neue Geleichung: 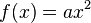 .
Mit der Manipulation des Schiebereglers hast du a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen. .
Mit der Manipulation des Schiebereglers hast du a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
Aufgabe 1
Hast du mit a etwas experimentiert?
Dann wird es dir jetzt nicht mehr schwer fallen, diese Sätze zu vervollständigen.
Ist a > 0, dann ist die Parabel enger (gestreckt) als die Normalparabel.
Für 0 < a < 1 ist die Parabel weiter (gestaucht) als die Normalparabel.
Ist a negativ, so ist die Parabel nach unten geöffnet .
Hast du die Aufgabe gelöst? Präge dir die jeweilige Auswirkung von a gut ein!
|
|
|
Mit deinen neugewonnenen Erkenntnissen kannst du die nächsten Aufgaben lösen.

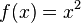 heißen Parabeln.
heißen Parabeln.
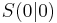 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
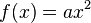 .
Mit der Manipulation des Schiebereglers hast du a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
.
Mit der Manipulation des Schiebereglers hast du a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
 Nächste Seite
Nächste Seite Zurück zur Übersicht
Zurück zur Übersicht
