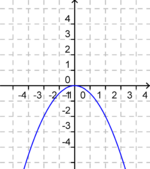
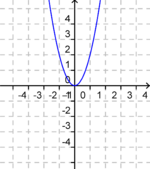
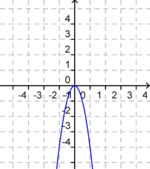
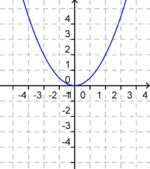
Der Graph der quadratischen Funktion "f(x) = ax²"
{ertfujhklökljhtghdrgtfhzjukhgcjffffffffffffffffffffffffffffffffffffffffffffffffffffff
Wenn man vom Scheitelpunkt aus eine Einheit nach rechts und 4 Einheiten nach oben geht, dann hat der Parameter a den Wert: (!1) (!2) (!3) (4)
</div>
4. Stelle nun den Schieberegler auf den Wert a = -2.
Funktioniert das Ablesen bei einem negativen Vorfaktor a genauso wie bei positiven Werten von a? (!Nein) (JA)
5. Man geht vom Scheitelpunkt aus eine Einheit nach rechts und drei Einheiten nach unten!
Wie lautet der Wert vom Vorfaktor a?? (!1) (-3) (!3)
|}
30px Merke
Anleitung zur Bestimmung des Vorfaktors a:
|
Um zu überprüfen, ob du die Vorgehensweise zum Finden des Vorfaktors a verstanden hast, versuche die nächste Aufgabe zu lösen.
Aufgabe:
Bestimme die Funktionsgleichung wie gerade erlernt!
Ordne Bilder und Funktionsgleichungen richtig zu!
 ax2"
ax2"
1. Aufgabe:
Um dir einmal zu zeigen, in welchen Bereichen des Alltags die Parabelform beispielsweise auftaucht, siehst du hier den Ausschnitt einer parabelförmigen Brückenaufhängung. Beantworte zuerst die folgende Frage und stelle dann den Graph durch Bedienen des Schiebereglers richtig ein!
Frage:
Was muss für den Vorfaktor a gelten? (Mehrere Antworten möglich!) (!er ist positiv) (er ist negativ) (!a < -1) (-1 < a < 0)
2. Aufgabe:
Gegeben ist die Funktionsvorschrift "f(x) = 0,5x2".
Im folgenden "GeoGebra-Applet" erkennst du die Punkte A, B, C und D. Diese Punkte können in y-Richtung verschoben werden. Ihr x-Wert hingegen ist fest vorgegeben. Überlege dir, welchen Wert der jeweilige y-Wert einnehmen muss und bewege den entsprechenden Punkt an diese Stelle. Überprüfe anschließend durch Anklicken des Kontrollkästchens "Graph", ob all deine Punkte auf dem Graph liegen. Liegen alle Punkte auf dem Graph, dann hast du die Aufgabe richtig gelöst!
3. Aufgabe:
Gegeben ist die quadratische Funktion "f(x) = ax2".
Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt ![[2|12]](/images/math/3/e/4/3e4074a68398eb26003d2c2ebec75ef9.png) verläuft? (!1) (!2) (3) (!4)
verläuft? (!1) (!2) (3) (!4)
Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt ![[3|9]](/images/math/b/3/b/b3bcc55d7f366e74bd38267bbdb0feec.png) verläuft? (1) (!2) (!3) (!4)
verläuft? (1) (!2) (!3) (!4)
Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt ![[4|32]](/images/math/1/a/4/1a464af0de9fda9d5f4c00cd158ff57e.png) verläuft? (!1) (2) (!3) (!4)
verläuft? (!1) (2) (!3) (!4)
Glückwunsch!
Damit hast du den Lernpfad "Der Graph der quadratischen Funktion f(x) ax2" abgeschlossen. Im folgenden und letzten Lernpfad werden schließlich alle Parameter und Darstellungsformen der quadratischen Funktion gemeinsam betrachtet und geübt. Viel Spaß!
ax2" abgeschlossen. Im folgenden und letzten Lernpfad werden schließlich alle Parameter und Darstellungsformen der quadratischen Funktion gemeinsam betrachtet und geübt. Viel Spaß!