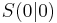|
Lernpfad
|
Die Quadratische Funktion der Form f(x) ax² ax²
Auf dieser Seite lernst du die die quadratischen Funktion mit dem Vorfaktor a! Bearbeite den unten aufgeführten Lernpfad
- Auswirkungen des Vorfaktors auf die Parabel für den positiven Vorfaktor a
- Auswirkungen des Vorfaktors auf die Parabel für den negativen Parameter a
- Auswirkungen des Vorfaktors a auf die Parabel auf einen Blick
- Aufstellen der Funktionsgleichung
- Aufgaben zum Einüben der quadratischen Funktion f(x)
 ax² ax²
|
|
Wie schon am Ende der Lerneinheit „Normalparabel“ angekündigt, werden wir die Normalparabel nun um einen Parameter erweitern.
Es kommt jetzt der Parameter a als „Vorfaktor“ hinzu, wodurch folgende Funktionsgleichung entsteht:
f(x)= a x²
x²
STATION 1: Auswirkungen des Vorfaktors auf die Parabel für den positiven Vorfaktor a
Bearbeite das folgende "Prettytable":
Quadratische Funktion f(x) ax2 ax2 |
Hinweise, Aufgabe und Lückentext:
|
|
|
Hinweise:
* In der Grafik ist die Normalparabel schwarz eingezeichnet und die von a abhängige quadratische Funktion blau.
* Bediene den roten Schieberegler mit der linken Maustaste, er verändert den Wert von a.
* Ziehe im Lückentext die möglichen Lösungen mit gehaltener linker Maustaste in die richtigen Felder.
Aufgabe:
Bediene den Schieberegler. Welche Veränderungen bewirkt der Faktor a an der quadratischen Funktion im Hinblick auf die Normalparabel?
Lückentext! - Ordne die richtigen Begriffe zu:
Der Vorfaktor a führt zu einer Streckung oder Stauchung der Normalparabel in Richtung der y-Achse.
Es findet jedoch keine Streckung oder Stauchung statt, wenn der Wert von a Eins beträgt, denn dann ist
f(x) = 1x² = x² identisch zur Normalparabel.
Ist a größer 1, so ist der Graph enger oder gestreckter als die Normalparabel.
Ist a hingegen kleiner 1, so ist der Graph weiter oder gestauchter als die Normalparabel.
Weiterhin gilt: Die quadratische Funktion f(x) = ax² ist nach oben geöffnet und der Scheitelpunkt S ist tiefster Punkt mit den Koordinaten 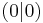 . .
|
 x²
x²
 ax2
ax2 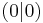 .
.