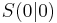Die quadratische Funktion der Form f(x) = ax²

Lernpfad Die Quadratische Funktion der Form f(x)$=$ax² Auf dieser Seite lernst du die die quadratischen Funktion mit dem Vorfaktor a! Bearbeite den unten aufgeführten Lernpfad Auswirkungen des Vorfaktors auf die Parabel für den positiven Parameter a Auswirkungen des Vorfaktors auf die Parabel für den negativen Parameter a Auswirkungen des Vorfaktors a auf einen Blick Aufstellen der Funktionsgleichung Aufgaben zum Einüben der quadratischen Funktion f(x)$=$ax²

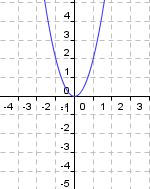
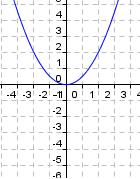
Wie schon am Ende der Lerneinheit „Normalparabel“ angekündigt, werden wir die Normalparabel nun um einen Parameter erweitern.

Es kommt jetzt der Parameter a als „Vorfaktor“ hinzu, wodurch folgende Funktionsgleichung entsteht:

f(x)= a$\cdot$x²

STATION 1: Auswirkungen des Vorfaktors auf die Parabel für den positiven Parameter a

Bearbeite das folgende "Prettytable":

Quadratische Funktion f(x)$=$ax2

Hinweise, Aufgabe und Lückentext:

Hinweise: * In der Grafik ist die Normalparabel schwarz eingezeichnet und die von a abhängige quadratische Funktion blau. * Bediene den roten Schieberegler mit der linken Maustaste, er verändert den Wert von a. * Ziehe im Lückentext die möglichen Lösungen mit gehaltener linker Maustaste in die richtigen Felder. Aufgabe: Bediene den Schieberegler. Welche Veränderungen bewirkt der Faktor a an der quadratischen Funktion im Hinblick auf die Normalparabel? Lückentext! - Ordne die richtigen Begriffe zu: Der Vorfaktor a führt zu einer                     der Normalparabel in Richtung der                     . Es findet jedoch keine Streckung oder Stauchung statt, wenn der Wert von a                     beträgt, denn dann ist f(x) = 1x² = x²                     zur Normalparabel. Ist a                     1, so ist der Graph enger oder gestreckter als die Normalparabel. Ist a hingegen kleiner 1, so ist der Graph                     als die Normalparabel. Weiterhin gilt: Die quadratische Funktion f(x) = ax² ist nach                     geöffnet und der                     S ist                     Punkt mit den Koordinaten $(0\!\,|\!\,0)$. y-AchseobentiefsterEinsStreckung oder Stauchungidentischgrößerweiter oder gestauchterScheitelpunkt

Merke Für die quadratische Funktion f(x)$=$ a$\cdot$x² mit dem positiven Faktor a gilt: Sie entsteht aus der Normalparabel durch eine Streckung oder Stauchung in Richtung der y-Achse Für a $=$ 1 gilt: Identisch zur Normalparabel, denn f(x)$=$ 1$\cdot$x²$=$ x² Für a > 0 gilt: Der Graph ist nach oben geöffnet Scheitelpunkt S ist tiefster Punkt und liegt im Ursprung $S(0\!\,|\!\,0)$ Für a > 1 ist der Graph enger/gestreckter als die Normalparabel Für a < 1 ist der Graph weiter/gestauchter als die Normalparabel

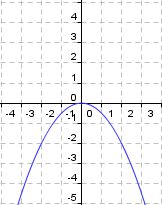
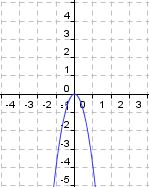
Nach dem wir den Fall für den positiven Vorfaktor a untersucht haben, schauen wir uns jetzt an, was passiert, wenn der Parameter a negativ wird.

STATION 2: Auswirkungen des Vorfaktors auf die Parabel für den negativen Parameter a

Bearbeite das folgende Quiz und lerne die Auswirkungen kennen, für den Fall das der Parameter a negativ wird!

Quadratische Funktion f(x) = ax², für positiven und negativen Parameter a:

Aufgabe und Quiz:

Aufgabe: Bediene wieder den Schieberegler. Welche Veränderungen bewirkt der Faktor a wenn er negativ wird? Quiz: In welche Richtung ist die Parabel für a < 0 geöffnet? Parabel ist nicht geöffnet nach oben nach unten Welche Aussage ist richtig? Scheitelpunkt S liegt im Ursprung und ist tiefster Punkt Scheitelpunkt S liegt im Ursprung und ist höchster Punkt Es gibt keinen Scheitelpunkt Was bewirkt der negative Vorfaktor a? Eine Streckung oder Stauchung Eine Streckung Eine Stauchung Was passiert wenn der Vorfaktor a = -1 ist? Die Parabel ist gestaucht Es liegt die identische Normalparabel vor, gespiegelt an der x-Achse Die Parabel ist nach oben geöffnet Für welche negativen a-Werte ist der Graph enger/gestreckter als die an der x-Achse gespiegelte Normalparabel? für a < -0,5 für a > -1 für a < -1 Für welche negativen a ist der Graph weiter/gestauchter als die Normalparabel? für -2 < a < 0 für a > -2 für 0 > a > -1 prüfen!

Merke Für die quadratische Funktion f(x)$=$ a$\cdot$x² mit dem negativen Faktor a gilt: Sie entsteht aus der Spiegelung an der x-Achse sowie durch eine Streckung oder Stauchung in Richtung der y-Achse Für a $=$ -1 gilt: Kongruente Normalparabel nach unten geöffnet; f(x)$=$-1$\cdot$x²$=$ -x² Für a < 0 gilt: Der Graph ist nach unten geöffnet Scheitelpunkt S ist höchster Punkt und liegt im Ursprung $S(0\!\,|\!\,0)$ Für a < -1 ist der Graph enger/gestreckter als die Normalparabel Für a > -1 ist der Graph weiter/gestauchter als die Normalparabel

STATION 3: Auswirkungen des Vorfaktors a auf einen Blick

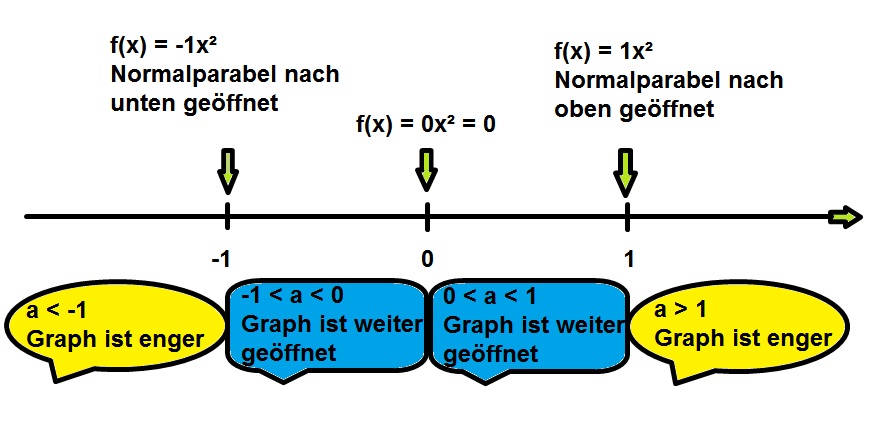
Da das nun einige Eigenschaften sowohl für den positiven als auch für den negativen Vorfaktor a waren, wollen wir diese mal zusammenfassen. Dabei soll dir die folgende Grafik helfen. Du wirst feststellen, es ist gar nicht so schwer!!

Aufgabe:

Versuche mit Hilfe der Grafik und deinem bisherigen Wissen das Memory-Puzzle zu lösen.

Scheitelpunkt S für negativen Parameter a a > 1 Vorfaktor a ist positiv Scheitelpunkt S für positiven Parameter a weiter/gestauchter Graph 0 < a < 1 Vorfaktor a ist negativ Graph ist weiter geöffnet Graph ist enger/gestreckter a < -1 0 > a > -1 Streckung oder Stauchung der Normalparabel tiefster Punkt, liegt im Ursprung

(0, 0)

Nach oben geöffnete Normalparabel Nach unten geöffnete Normalparabel enger/gestreckter Graph höchster Punkt, liegt im Ursprung

(0, 0)

Der Vorfaktor a bewirkt eine…

STATION 4: Aufstellen der Funktionsgleichung

Bisher hast du ja immer den Wert des Vorfaktors a an der Grafik ablesen können. Nun wollen wir mal schauen wie man anhand eines Graphen den Parameter a bestimmt.

Betrachte hierfür die dargestellte Grafik und versuche mit Hilfe der gemachten Angaben die Funktionsgleichung selbstständig aufzustellen:

Quadratische Funktion f(x) = ax², für positiven und negativen Parameter a:	Aufgabe und Quiz:
	1. Lies die Koordinaten eines frei gewählten Punktes. Achtung: Nimm nicht den Scheitelpunkt 2. Füge den x- und den y-Wert in die Funktionsgleichung f(x) = ax² ein. Hinweis: f(x) = y 3. Löse die aufgestellte Gleichung nach a auf. Wie ist dein Ergebnis? A) f(x) = 5x² B) f(x) = 2x² C) f(x) = 3x² [Lösung anzeigen][Lösung ausblenden] f(x) $=$2x2

Um zu überprüfen, ob du die Vorgehensweise zum Finden des Parameters a verstanden hast, versuche die nächste Übung zu lösen.

Übung:

Bestimme die Funktionsgleichung wie gerade erlernt!

Ordne Bilder und Funktionsgleichungen richtig zu!

f(x) = 0x²

f(x) = 2x².jpg

f(x) = 0,5x²

f(x) = -4x²

f(x) = 0,5x²

´

STATION 5: Aufgaben zum Einüben der quadratischen Funktion f(x)$=$ax²

1. Aufgabe:

Für diese Aufgabe hast du eine Parabel aus dem Alltag vorgegeben. Die Brückenkonstruktion beruht auf einer Parabelform die noch mal zur Verdeutlichung schwarz eingezeichnet wurde. Stelle hierfür eine Funktionsgleichung auf: