Höhen im Dreieck
Aus DMUW-Wiki
Version vom 14. Juli 2009, 09:40 Uhr von Anja Ebert (Diskussion | Beiträge)
Höhen im Dreieck
- Auch hier darfst Du wieder konstruieren.
- Öffne wieder die Geogebra Datei durch Klick auf den Button. Konstruiere eine Höhe im dem vorgegebenen Dreieck, nach folgender Aufgabenstellung:
- Zeichne vom Punkt C aus eine senkrechte Gerade zur gegenüberliegenden Seite c des Dreiecks.
- Schneide wieder diese Gerade mit der Seite c.
- Blende die Gerade aus!
- Konstruiere eine Strecke zwischen dem erhaltenen Schnittpunkt und der Ecke C.
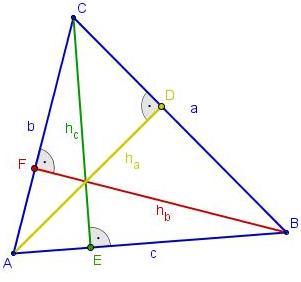
Sehr schön! Was Du konstruiert hast ist eine Höhe des Dreiecks vom Eckpunkt C aus, auf die gegenüberliegende Seite.
- 5. Bewege den Eckpunkt C nach Links und Rechts. Was passiert mit der Höhe?
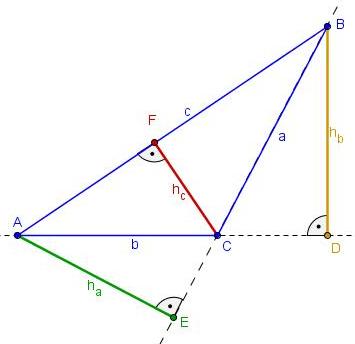
Bewegt man den Eckpunkt C so weit, dass ein Basiswinkel (nicht der Winkel am Eckpunkt C) größer als 90° wird, so liegt die Höhe außerhalb des Dreiecks! Dies ist in stumpfwinkligen Dreiecken der Fall!
- So löst man das Problem:
- Konstruiere eine Gerade durch A und B
- Zeichne eine Senkrechte vom Punkt C zu dieser Geraden!
- Schneide diese Senkrechte Gerade mit der Geraden durch AB. Blende die Senkrechte Gerade wieder aus.
- Verbinde den erhaltenen Schnittpunkt mit C
- Was Du nun konstruiert hast, ist wieder eine Höhe vom Eckpunkt C aus. Doch diese kann auch außerhalb liegen!! Teste dies durch Bewegen von C!!
Zusammenfassung: Höhen im Dreieck
- Auch die Eigenschaften der Höhen im Dreieck solltest du wissen. Daher wurden sie hier zusammengefasst. Wenn Du möchtest, kannst Du den Merkkasten in Dein Heft übrtragen.