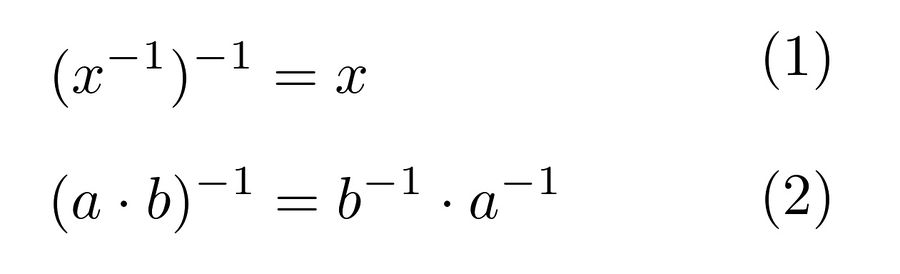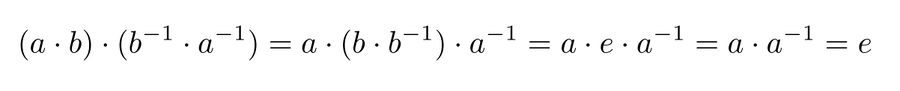Shoes and Socks

Aussage

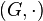Sei $(G,\cdot)$ eine Gruppe (d.h. abgeschlossene zweistellige Verknüpfung, Assoziativität, neutrales Element, inverse Elemente), dann gilt für alle $x, a, b \in G$:

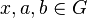Beweis

1. Doppelte Invertierung eines Gruppenelements

2. Shoes and Socks

Aspekte

• Wir können die beiden Aussagen auch nachrechnen:

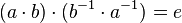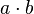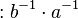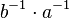Wir haben gezeigt, dass $(a \cdot b) \cdot (b^{-1} \cdot a^{-1}) = e$, d.h. $a \cdot b$ ist ein linksinverses Element von $:b^{-1} \cdot a^{-1}$ und $b^{-1} \cdot a^{-1}$ ist ein rechtsinverses Element von $a \cdot b$.

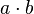Wir wissen mit der Aussage über die Abschwächung der Gruppendefinition, dass in einer Gruppe die Begriffe rechts- und :linksinvers zusammenfallen. Sobald das eine gegeben ist, dann ist auch das andere gegeben.

Genauso wissen wir mit der Aussage über die Eindeutigkeit der inversen Elemente in einer Gruppe, dass das Gruppenelement 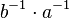$b^{-1} \cdot a^{-1}$ das einzige zu 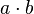$a \cdot b$ inverse Element ist.

• Genauso gilt:

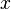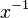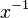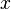Wir können die Aussage so lesen: $x$ ist linksinvers zu $x^{-1}$. Genauso gilt aber auch: $x^{-1}$ ist rechtsinvers zu $x$.