Untergruppenkriterium
Aus DMUW-Wiki
Version vom 27. November 2018, 15:53 Uhr von Kilian Schoeller (Diskussion | Beiträge)
Aussage
Sei 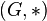 eine Gruppe und U eine Teilmenge von G, also
eine Gruppe und U eine Teilmenge von G, also 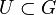 . Dann gilt:
. Dann gilt:
Definitionen
Was bedeutet "mit der eingeschr\"ankten Verkn\"upfung von G auf U"? G ist eine Gruppe, d.h. es gibt eine Verknüpfung auf G, also eine Abbildung 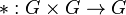 .
.
Wir haben eine Abbildung, d.h. wir können Einschränkungen dieser Abbildung betrachten. In unserem Fall betrachten wir 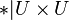 .
Ist U mit dieser Einschränkung eine Gruppe (Abgeschlossenheit + Assoziativität + neutrales Element + inverse Elemente), dann sagen wir: U ist eine Untergruppe von G und schreiben:
.
Ist U mit dieser Einschränkung eine Gruppe (Abgeschlossenheit + Assoziativität + neutrales Element + inverse Elemente), dann sagen wir: U ist eine Untergruppe von G und schreiben: 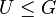
Beweis
Es liegt eine Äquivalenz vor, d.h. wir müssen zwei Implikationen zeigen:
1. 


