Algebra: quadratische Funktionen
Du hast dich viel mit quadratischen Funktionen, deren Graphen, Nullstellen, Scheiteln etc beschäftigt. Wie sieht eine quadratische Funktion noch einmal aus? Eine "tanzende" Parabel siehst du hier:
Das ist der Graph einer quadratischen Funktion der Form y = ax2 + bx + c, bei der sich die Parameter a,b und c ständig verändern! Wenn du willst, kannst du die Animation per Mausklick anhalten und dir überlegen, wie die passende quadratische Gleichung zu dem Graphen lautet!
Finde die versteckten Begriffe zu quadratischen Funktionen
Finde die Wörter, indem du diese mit der linken Maustaste markierst. Klicke auf den ersten Buchstaben des Wortes, halte die linke Maustaste gedrückt und bewege den Cursor über das Wort! (Waagrecht, senkrecht und auch schräg, gefundene Wörter werden grün markiert.)
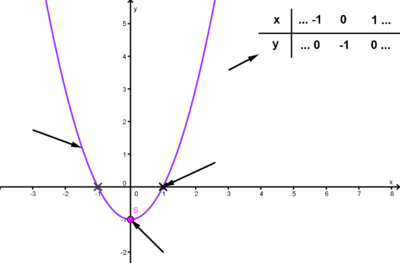
Falls du Hilfe brauchst: Unter dem Suchsel findest du noch eine kleine Grafik, damit du weißt, nach welchen Begriffen du Ausschau halten musst!
| Scheitel |
| Parabel |
| Nullstelle |
| Wertetabelle |
Hilfe
Memo-Quiz zu quadratischen Funktionen und deren Funktionsgraphen
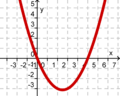
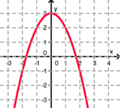
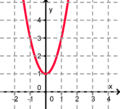
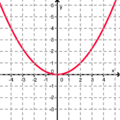
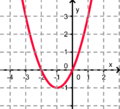
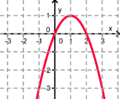
Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen). Unter dem Memo-Quiz findest du noch eine kleine Hilfestellung!
Das ist ein Beispiel für ein richtiges Paar: 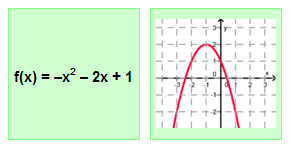
Dieses Geogebra Applet kann dir dabei helfen, dir die verschiedenen Graphen vorzustellen! Bewege einfach die Schieberegler, um die Parameter a, b und c zu verändern... dadurch veränderst du die Parabel p!
 Weiter zu 9. Klasse Geometrie
Weiter zu 9. Klasse Geometrie Zurück zu 8. Klasse Geometrie
Zurück zu 8. Klasse Geometrie
