Geometrie: Flächensätze am rechtwinkligen Dreieck
Aus DMUW-Wiki
Flächensätze am rechtwinkligen Dreieck
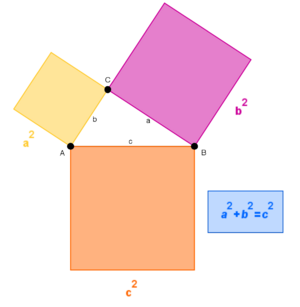
Den Satz a2 + b2 = c2 hast du im Unterricht bereits kennengelernt.
Nach wem wurde dieser Satz noch einmal benannt?
Mit diesem Satz kannst du in rechtwinkligen Dreiecke die Länge einer Strecke c berechnen, wenn die beiden anderen a und b gegeben sind. Wie rechtwinklige Dreiecke aussehen können, siehst du hier:
Du kannst die Animation jederzeit anhalten, um die errechneten Werte zu vergleichen und zu überprüfen!
Beim Klick auf die Ziffern im Kreuzworträtsel öffnet sich ein Eingabefeld zum Eintragen.
| 6 | |||||||||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 5 | 9 | ||||||||
Benutzen Sie zur Eingabe die Tastatur. Eventuell müssen sie zuerst ein Eingabefeld durch Anklicken aktivieren.
- Senkrecht
- Pythagoras war Philosoph und ...1
- Wie hieß der Geheimbund, den er um 530 v.Chr. gründete?6
- In welchem Land wurde Pythagoras geboren?8
- Die längste Seite im rechtwinkligen Dreieck9
- Waagrecht
- a ... plus a ... ist c ...2
- Strecke zwischen Dreiecksecke und Lotfußpunkt3
- Die beiden kürzeren Seiten im rechtwinkligen Dreieck (Plural!)4
- Ein Winkel mit 90° heißt auch ... Winkel5
- Dieser Mathematiker entdeckte den Höhensatz7
Setze das Puzzle zusammen. Präge dir dabei die Zeichnung gut ein. Viel Spaß dabei!
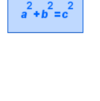
Weiter zu 10. Klasse Algebra
Zurück zu 9. Klasse Algebra
