Grundlagen der Zerlegungsgleichheit von Figuren

Auf dieser Seite lernst Du die Eigenschaften der Zerlegungsgleichheit von Figuren kennen.

Bearbeite die Aufgaben sorgfältig!
Nicht mogeln...schaue erst die Lösungen an, wenn du die Aufgaben selbstsändig bearbeitet hast! Denn nur so lernst du am Besten!

1.Station Wiederholung des Kongruenzbegriffes

Weißt Du noch was man unter 'Kongruenz von Figuren versteht??

Eine Wiederholung kann sicher nicht schaden.

Teste Dein Wissen!

Ein anderes Wort für Kongruenz ist Deckungs-gleichheit

Hinweis: Kongruente Figuren kann man zur Deckung bringen

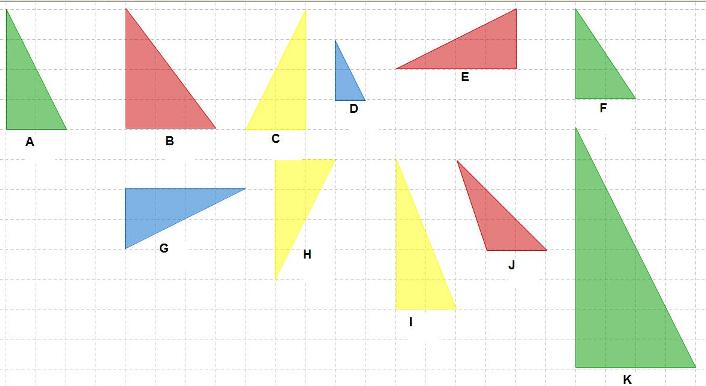
Aufgabe: Kongruente Dreiecke

Findest Du alle Dreiecke, die zum Dreieck A kongruent sind?
''Gib die Buchstaben an.''

0-1 Punkt: Versuche die Aufgabe noch einmal.
2 Punkte: Sehr gut gemacht!

War Deine Lösung richtig?

2. Station: Wie erzeugt man kongruente Figuren?

In dieser Darstellung siehst Du drei Möglichkeiten, wie man kongruente Figuren erzeugen kann.
Dreieck A, B, C und D sind kongruent zueinander.
Wie kann man die Dreiecke B, C und D ausgehend vom Dreieck A erzeugen?

Im 1. Schritt wird das Dreieck an einer Achse gespiegelt. Diese Spiegelachse kannst Du an den roten Punkten ändern. Beobachte wie sich das gespiegelte Dreieck verändert.

Im 2. Schritt kannst Du das Dreieck verschieben

Im 3. Schritt kannst Du das Dreieck drehen. Der Winkel zeigt Dir dabei an, um wieviel Grad Du das Dreieck drehst.

Spiegelungen, Drehungen und Verschiebungen nennt man Kongruenzabbildungen, da die Bildfiguren in allen Maßen mit der Ausgangsfigur übereinstimmen. Bildfigur und Ausgangsfigur sind kongruent zueinander

3.Station: Das sollest Du also wissen

Maja hat die Eigenschaften von kongruenten Figuren aufgeschrieben. Doch ein Sturm hat manche Wörter durcheinander gebracht.
Kannst Du sie wieder ordnen?

Zwei Figuren sind zueinander kongruent, wenn sie durch Verschiebung,Drehung oder Spiegelung
ineinander überführt werden können.
Diese drei Abbildungen nennt man daher auch Kongruenz-abbildungen.
Kongruente Figuren haben den gleichen Flächeninhalt.

4.Station: Wofür können wir die Kongruenz von Figuren gebrauchen?

Du kennst sicher ein paar Anwendungsbeispiele wofür man die Eigenschaften der man die Kongruenz von Figuren nutzen kann.

Dazu gehört zum Beispiel die Konstruktion von Dreiecken, wofür man die Kongruenzsätze benötigt. Kennst Du noch alle davon?

Ordne die richtige Abkürzung der Beschreibung zu!

Zwei Dreiecke, die in ihren drei Seitenlängen übereinstimmen, sind kongruent: SSS-Satz
Zwei Dreiecke, die in einer Seitenlänge und in den dieser Seite anliegenden Winkeln übereinstimmen, sind kongruent: WSW-Satz
Zwei Dreiecke, die in zwei Seitenlängen und in dem eingeschlossenen Winkel übereinstimmen, sind kongruent: SWS-Satz
Zwei Dreiecke, die in zwei Seitenlängen und in jenem Winkel übereinstimmen, der der längeren Seite gegenüberliegt, sind kongruent: SsW-Satz

Prima! Das war schon die erste Seite des Lernpfads. Das ging ja fix.'

Im dem nächsten Abschnitt lernst Du ein weiteres Anwendungsbeispiel für die Kongruenz kennen

Hier geht es weiter:

→Zerlegungsgleichheit von Figuren

	B und D
	C und E
	G und H
	J und K
	I und F

Grundlagen der Zerlegungsgleichheit von Figuren