Übung zur Zerlegungsgleichheit

Aufgabe 1 zum Aufwärmen

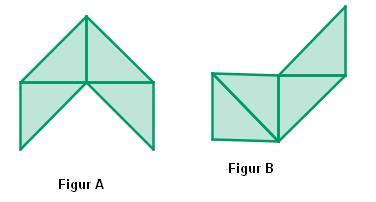
Begründe, warum die folgenden Figuren A und B den gleichen Flächeninhalt besitzen:

Hier siehst Du Majas Lösung. Ist sie richtig? [Anzeigen][Verstecken]

Figur A und B sind zueinander zerlegungsgleich. Sie bestehen aus je 4 zueinander kongruenten Teildreiecken. Damit besitzen sie den gleichen Flächeninhalt.

---

Aufgabe 2 für Geübte: Ergänzungsgleiche Figuren

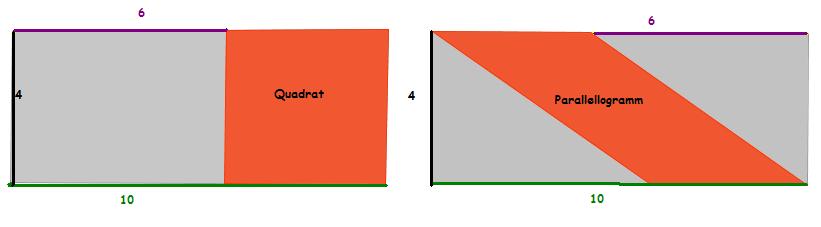
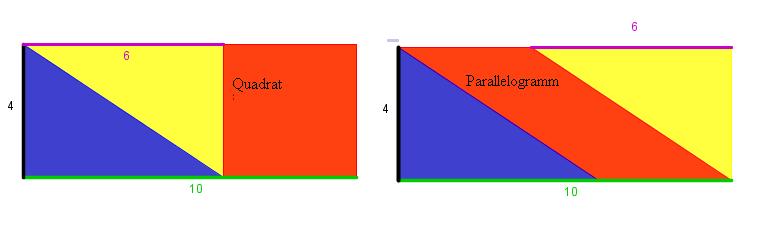
Zwei Rechtecken mit der Länge 10cm und der Breite 4cm ist ein Quadrat und ein Parallelogramm einbeschrieben.

Was haben Quadrat und Parallelogramm gemeinsam?

Tipp:[Anzeigen][Verstecken]

Überlege, wie man das linke und das rechte Rechteck geeignet zerlegen kann.

Beantworte dazu die Fragen:

1. Haben Quadrat und Parallelogramm den gleichen Umfang?

	ja
	nein

2. Sind Quadrat und Parallelogramm ergänzungsgleiche Figuren?

	ja
	nein

3. Besitzen Quadrat und Parallelogramm den gleichen Flächeninhalt?

	ja
	nein

4. Sind Quadrat und Parallelogramm zerlegungsgleich?

	nein
	ja

Punkte: 0 / 0

Bist Du ganz sicher, dass Du den Hinweis von Nils brauchst?

[Anzeigen][Verstecken]

---

Aufgabe 3 für Profis: Wunderliche Parallelogramme

• [BD] ist die Diagonale.
• [FK] eine Parallele zur Seite [BC] und [LM] eine Parallele zu [AB]
• Sie schneiden sich im Punkt S

" Die Parallelogramme SLAF und MCKS besitzen den gleichen Flächeninhalt!"

Hat Nils Recht? Du kannst S variieren. Beobachte, wie sich Teilfiguren ändern. 1. Welches Parallelogramm halbiert die Diagonale? Das Parallelogramm ABCD Das Parallelogramm SMCK Das Parallelogramm SFDM Das Parallelogramm ADML Das Parallelogramm LSKB 2. Welche Dreiecke sind kongruent zueinander? Dreieck BCD und Dreieck BAD Dreieck SKB und Dreieck BAD Dreieck DMS und Dreieck SLB Dreieck DMS und Dreieck BFS Dreieck SKB und Dreieck SLB Punkte: 0 / 0

Dreieck DMS und DFS sind kongruent zueinander. Ebenso Dreieck SKB und SLB. Entfernt man diese Dreiecke von den kongruenten Dreiecken BAD und BCD, so haben die Restfiguren SLAF und SMCK den gleichen Flächeninhalt. 1. Die Parallelogramme SLAF und SMCK besitzen den gleichen Flächeninhalt ja nein Punkte: 0 / 0

---

Get more and explore:

Gratuliere, Du hast den 1. Lernpfad erfolgreich bearbeitet!
Du kennst Dich jetzt schon sehr gut mit zerlegungsgleichen Figuren aus und bist fit die Flächeninhaltsformel von Figuren zu entdecken.

Nils und Maja begleiten dich dabei wieder:

→Hier geht es weiter zum 2. Lernpfad

Hier geht es zurück zur Zusammenfassung zur Zerlegungsgleichheit