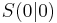Die quadratische Funktion der Form f(x) = ax²
|
Lernpfad
|
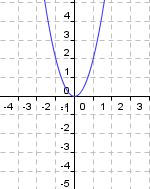
Wie schon am Ende der Lerneinheit „Normalparabel“ angekündigt, werden wir die Normalparabel nun um einen Parameter erweitern.
Es kommt jetzt der Parameter a als „Vorfaktor“ hinzu, wodurch folgende Funktionsgleichung entsteht:
f(x)= ax²
Bearbeite das folgende Arbeitsblatt:
Quadratische Funktion f(x) ax2 ax2 |
Hinweise, Aufgabe und Lückentext: |
|---|---|
|
Hinweise:
Der Vorfaktor a führt zu einer Streckung oder Stauchung der Normalparabel in Richtung der y-Achse. |
30px Merke
Für die quadratische Funktion f(x)
|
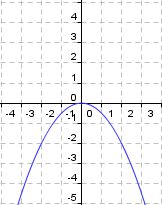
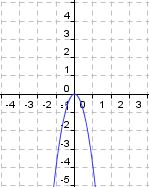
Nach dem wir den Fall für den positiven Vorfaktor a untersucht haben, schauen wir uns jetzt an, was passiert, wenn der Parameter a negativ wird.
Bearbeite das folgende Quiz und lerne die Auswirkungen kennen, wenn der Parameter a negativ wird!
| Quadratische Funktion f(x) = ax², für positiven und negativen Parameter a: | Aufgabe und Quiz: |
|---|---|
| Aufgabe: Bediene wieder den Schieberegler. Welche Veränderungen bewirkt der Faktor a wenn er negativ wird? Quiz: In welche Richtung ist die Parabel für a < 0 geöffnet? (!Parabel ist nicht geöffnet) (!nach oben) (nach unten) Welche Aussage ist richtig? (!Es gibt keinen Scheitelpunkt) (!Scheitelpunkt S liegt im Ursprung und ist tiefster Punkt) (Scheitelpunkt S liegt im Ursprung und ist höchster Punkt) Was bewirkt der negative Vorfaktor a? (!Eine Streckung) (!Eine Stauchung) (Eine Streckung oder Stauchung) Was passiert wenn der Vorfaktor a = -1 ist? (Es liegt die identische Normalparabel vor, gespiegelt an der x-Achse) (!Die Parabel ist nach oben geöffnet) (!Die Parabel ist gestaucht) Für welche negativen a-Werte ist der Graph enger/gestreckter als die an der x-Achse gespiegelte Normalparabel? (!für a < -0,5) (!für a > -1) (für a < -1) Für welche negativen a ist der Graph weiter/gestauchter als die Normalparabel? (!für a > -2) (für 0 > a > -1) (!für -2 < a < 0) |
30px Merke
Für die quadratische Funktion f(x)
|
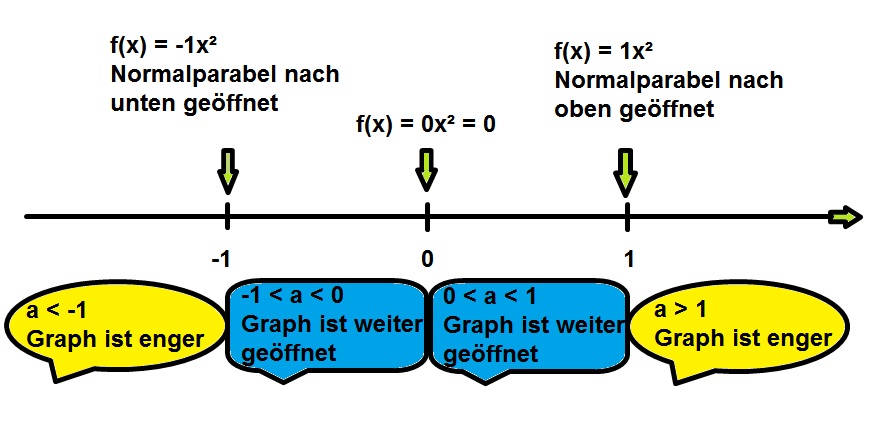
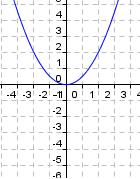
Da das nun einige Eigenschaften sowohl für den positiven als auch für den negativen Vorfaktor a waren, wollen wir diese mal zusammenfassen. Dabei soll dir die folgende Grafik helfen. Du wirst feststellen, es ist gar nicht so schwer!!
Aufgabe:
Versuche mit Hilfe der Grafik und deinem bisherigen Wissen das Memory-Puzzle zu lösen.
| Vorfaktor a ist negativ | Nach unten geöffnete Normalparabel |
| Vorfaktor a ist positiv | Nach oben geöffnete Normalparabel |
| a < -1 | enger/gestreckter Graph |
| 0 > a > -1 | weiter/gestauchter Graph |
| a > 1 | Graph ist enger/gestreckter |
| 0 < a < 1 | Graph ist weiter geöffnet |
| Scheitelpunkt S für negativen Parameter a | Scheitelpunkt ist höchster Punkt und liegt im Ursprung
(0, 0) |
| Scheitelpunkt S für positiven Parameter a | Scheitelpunkt ist tiefster Punkt und liegt im Ursprung
(0, 0) |
| Der Vorfaktor a bewirkt eine… | Streckung oder Stauchung der Normalparabel |
Bisher hast du ja immer den Wert des Vorfaktors a an der Grafik ablesen können. Nun wollen wir mal schauen wie man anhand eines Graphen den Parameter a bestimmt.
Betrachte hierfür die dargestellte Grafik und versuche mit Hilfe der gemachten Angaben die Funktionsgleichung selbstständig aufzustellen:
| Quadratische Funktion f(x) = ax², für positiven und negativen Parameter a: | Aufgabe und Quiz: |
|---|---|
|
1. Lies die Koordinaten eines frei gewählten Punktes.
A) f(x) = 5x² B) f(x) = 2x² C) f(x) = 3x²
f(x)
|
Um zu überprüfen, ob du die Vorgehensweise zum Finden des Parameters a verstanden hast, versuche die nächste Übung zu lösen.
Übung:
Bestimme die Funktionsgleichung wie gerade erlernt!
Ordne Bilder und Funktionsgleichungen richtig zu!
 ax²
ax²
1. Aufgabe:
Für diese Aufgabe hast du eine Parabel aus dem Alltag vorgegeben. Du siehst hier einen Ausschnitt einer Kirche und die Parabelform die hier vorkommt, sie ist schwarz eingezeichnet. Stelle hierfür eine Funktionsgleichung auf:
Lösung:
- Deine Lösung für a sollte ungefähr -0,1 betragen, damit ergibt sich die Funktionsgleichung: f(x) -0,1x2
-0,1x2
- Hattest du Probleme mit dem Finden des Parameters a, dann geh nochmal zurück zu Station 4
2. Aufgabe - KNIFFELAUFGABE:
Nachdem du nun weißt wie man am Graphen die Funktionsvorschrift abliest, fällt es dir auch sicher auch nicht schwer einen Graphen selbst zu zeichnen, von dem du die Funktionsvorschrift kennst.
Nimm dir ein Blatt Papier und zeichne die Graphen für folgende Funktionsvorschriften:
a) f(x) = 3x²
b) g(x) = -2x²
Hilfe:
Falls du nicht weißt was du machen sollst, kannst du dir hier eine Hilfe holen!
- Gebe dir einen x-Wert in der Gleichung vor und finde den dazugehörigen y-Wert.
z.B. für x  1 ist y
1 ist y  3
3 (1)²
(1)²  3
- Suche mehrere Punkte und verbinde diese
3
- Suche mehrere Punkte und verbinde diese
Lösung:
Nachdem man sich mehrere Koordinaten errechnet hat, kann man diese ins Koordinatensystem eintragen und die Punkte verbinden.
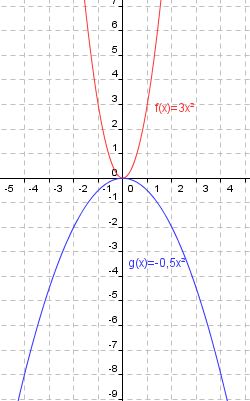
3. Aufgabe:
Die Funktion f hat die Gleichung f(x) = ax². Bestimme den Faktor a wenn der Graph f durch den Punkt 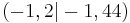 verläuft
verläuft
Tipp! Ähnlich zur 2. Aufgabe
Lösung:
f(x) ax2 und P
ax2 und P 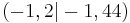
→ -1,44 a
a (-1,2)2
(-1,2)2
Umstellen nach a ergibt: 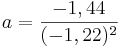
→ a 1
1
4. Aufgabe:
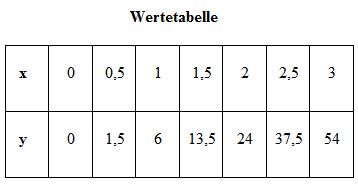
Ein Junge spuckt von einer Brücke und misst die Zeit und den zugehörigen Weg wie in der Tabelle dargestellt.
Dabei ist der x-Wert die Strecke und der y-Wert ist die Zeit.
Stelle die Funktionsvorschrift in der Form f(x) = ax² auf.
Lösung:
Man nimmt sich einen beliebigen Punkt, z.B. P 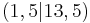 und berechnet den Parameter a:
und berechnet den Parameter a:
13,5 a
a (1,5)2
(1,5)2
→ a 6
6
→ f(x) 6
6 x2
x2
 .
.