Zusammenfassung: Flächeninhalt des Dreiecks
Übertrage den roten Merkkasten in dein Heft, damit Du die Flächeninhaltsformel für Dreiecke auch Zuhause nachschauen kannst:
 |
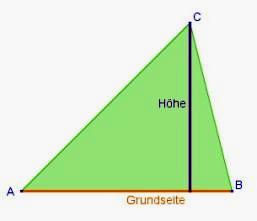
Den Flächeninhalt des Dreiecks berechnet man durch
mit g als Grundseite und h als der dazugehörigen Höhe. |
|
Aber Moment! Da fehlt doch noch was
 Maja kennt sich mit Dreiecken aus.
Maja kennt sich mit Dreiecken aus.
Sie weiß, dass es ganz spezielle Dreiecke gibt.
Wie sieht die Formel dafür aus?
Bearbeite dazu den nächsten Abschnitt
Variation am Dreieck
- Du siehst hier ein Dreieck, bei dem die Seiten gegeben sind:
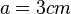 ,
, 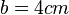
und 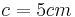
- Maja will den Flächeninhalt des Dreiecks ABC berechnen.
- Welches spezielle Dreieck ist das Dreieck ABC?
Schaffst Du es auch ohne den zweiten Hinweis?
- Ist nicht schon eine Höhe gegeben, die Maja verwenden kann?
- Zeig den Hinweis von Nils im Applet an
- Berechne den Flächeninhalt des Dreiecks
Es gilt zum Beispiel:
Länge Grundseite b: 4 (cm)
Länge der zugehörigen Höhe a : 3 cm
Der Flächeninhalt des Dreiecks beträgt 12(cm²)
Nils hat die Formel für die Berechnung dieses speziellen Dreiecks zusammengefasst:
 |
Der Flächeninhalt eines rechtwinkligen Dreiecks berechnet sich durch :
wobei a und b senkrecht zu einander stehen.
|
Wie lautet die Flächeninhaltsformel für ein
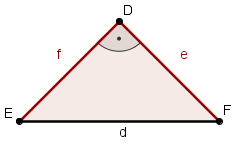
- ..gleichschenklig-rechtwinkliges Dreieck ABC ?
- Der rechte Winkel befindet sich am Eckpunkt D.
Flächeninhalt von stumpfwinkligen Dreiecken
|
Spitze! Du hast die Aufgabe prima bearbeitet

→Übungsaufgaben zur Flächenberechnung am Dreieck
Zurück zur Seite
Die Flächeninhaltsformel des Dreiecks
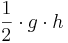


 Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt:
Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt:

