Algebra: Potenzen und Potenzfunktionen
Aus DMUW-Wiki
Potenzen und Potenzfunktionen
Potenzen und Potenzgesetze hast du schon kennengelernt.
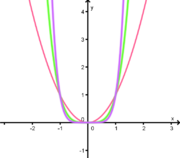
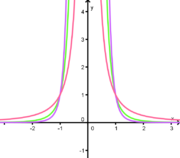
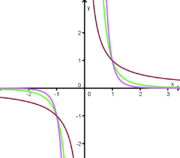
Durch Klick auf "Anzeigen" siehst du eine Potenzfunktion der Form y = xa.
Du kannst mit dem Schieberegler den Parameter a der Gleichung variieren: 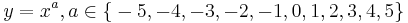
|
|

 Weiter zu 10. Klasse Geometrie
Weiter zu 10. Klasse Geometrie Zurück zu 9. Klasse Geometrie
Zurück zu 9. Klasse Geometrie
