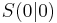Streckung, Stauchung und Spiegelung der quadratischen Funktion

Lernpfad Streckung, Stauchung und Spiegelung der quadratischen Funktion In diesem Lernpfad lernst du die quadratische Funktion mit dem Vorfaktor a kennen! Bearbeite den unten aufgeführten Lernpfad! Auswirkungen des Vorfaktors auf die Normalparabel für den positiven Parameter a Auswirkungen des Vorfaktors auf die Normalparabel für den negativen Parameter a Auswirkungen des Vorfaktors a auf einen Blick Aufstellen der Funktionsgleichung Aufgaben zum Einüben der quadratischen Funktion f(x)$=$ax²

In dieser Lerneinheit lernst du nun den letzten Parameter kennen, der die Parabel verändert. Wie schon in der Überschrift genannt, sorgt dieser Parameter für eine Streckung, Stauchung und/oder eine Spiegelung. Wie das genau funktioniert lernst du in den nächsten Station kennen.

Aber nun erstmal zur Funktionsgleichung. Der Parameter a kommt als "Vorfaktor" dazu, wodurch die folgende Funktionsgleichung entsteht:

                         f(x)= a$\cdot$x²

Bevor wir uns mit den Auswirkungen des Vorfaktors beschäftigen, müssen wir die Begriffe "Streckung", "Stauchung" und "Spiegelung" erläutern, damit jeder weiß, was damit gemeint ist.

Überlege dir, was du unter den Begriffen verstehst, und löse dann die folgende Aufgabe.

Aufgabe:

Du hast verschiedene Bilder vorgegeben. Ordne die richtigen Begriffe zu!

ÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄNNNNNNNNNNNNNNNDDDDDDDDDDDDDDDDEEEEEEEEEEEEEEERRRRRRRRRRRRRRRNNNNN

gestreckt		gestaucht		gespiegelt		nicht gespiegelt		normal

__________________________________________________________________________________

STATION 1: Auswirkungen des Vorfaktors auf die Normalparabel für den positiven Parameter a

Bearbeite das folgende Arbeitsblatt:

Quadratische Funktion f(x)$=$ax2

Hinweise, Aufgabe und Lückentext:

Hinweise: * In der Grafik ist die Normalparabel schwarz eingezeichnet und die von a abhängige quadratische Funktion blau * Bediene den roten Schieberegler mit der linken Maustaste, er verändert den Wert von a * Ziehe im Lückentext die möglichen Lösungen mit gehaltener linker Maustaste in die richtigen Felder Aufgabe: Bediene den Schieberegler. Welche Veränderungen bewirkt der Faktor a an der quadratischen Funktion im Hinblick auf die Normalparabel? Lückentext! - Ordne die richtigen Begriffe zu: Der Vorfaktor a führt zu einer Streckung oder Stauchung der Normalparabel in y-Richtung. Es findet jedoch keine Streckung oder Stauchung statt, wenn der Wert von a Eins ist, denn dann ist f(x) = 1x² = x² identisch zur Normalparabel. Ist a größer 1, so ist der Graph im Vergleich zur Normalparabel gestreckt. Ist a hingegen kleiner 1, so nennt man den Graph gestaucht. Außerdem ist die quadratische Funktion f(x) = ax² nach oben geöffnet und der Scheitelpunkt S ist tiefster Punkt mit den Koordinaten $(0\!\,|\!\,0)$.

Merke Für die quadratische Funktion f(x)$=$ a$\cdot$x² mit dem positiven Faktor a gilt: Die von a abhängige Parabel entsteht aus der Normalparabel durch eine Streckung oder Stauchung in y-Richtung Für a $=$ 1 gilt: Identisch zur Normalparabel, denn f(x)$=$ 1$\cdot$x²$=$ x² Für a > 0 gilt: Der Graph ist nach oben geöffnet Scheitelpunkt S ist tiefster Punkt und liegt im Ursprung $S(0\!\,|\!\,0)$ Für a > 1 ist der Graph im Vergleich zur Normalparabel gestreckt Für a < 1 ist der Graph im Vergleich zur Normalparabel gestaucht

Nach dem wir den Fall für den positiven Vorfaktor a untersucht haben, schauen wir uns jetzt an, was passiert, wenn der Parameter a negativ wird.

STATION 2: Auswirkungen des Vorfaktors auf die Normalparabel für den negativen Parameter a

Bearbeite das folgende Quiz und lerne die Auswirkungen kennen, wenn der Parameter a negativ wird!

Quadratische Funktion f(x) = ax², für positiven und negativen Parameter a:

Aufgabe und Quiz:

Aufgabe: Bediene wieder den Schieberegler. Welche Veränderungen bewirkt der Faktor a, wenn er negativ wird? Quiz: Wie ist die Parabel geöffnet für a < 0? (!gar nicht) (!nach oben) (nach unten) Welche Aussage ist richtig? (!Es gibt keinen Scheitelpunkt) (!Der Scheitelpunkt S liegt im Ursprung und ist tiefster Punkt) (Der Scheitelpunkt S liegt im Ursprung und ist höchster Punkt) Was bewirkt der negative Vorfaktor a? (!Eine Streckung) (!Eine Stauchung) (Eine Streckung oder Stauchung) Was passiert wenn der Vorfaktor a = -1 ist? (Es liegt die an der x-Achse gespielte Normalparabel vor) (!Die Parabel ist nach oben geöffnet) (!Die Parabel ist gestaucht) Für welche negativen Werte von a, ist der an der x-Achse gespiegelte Graph gestreckt? (!für a < -0,5) (!für a > -1) (für a < -1) Für welche negativen Werte von a, ist der an der x-Achse gespiegelte Graph gestaucht? (!für a > -2) (für 0 > a > -1) (!für -2 < a < 0)

Merke Für die quadratische Funktion f(x)$=$ a$\cdot$x² mit dem negativen Faktor a gilt: Sie von a abhängige Parabel entsteht aus der Spiegelung an der x-Achse sowie einer Streckung oder Stauchung in y-Richtung Für a $=$ -1 gilt: Kongruente Normalparabel nach unten geöffnet; f(x)$=$-1$\cdot$x²$=$ -x² Für a < 0 gilt: Der Graph ist nach unten geöffnet Scheitelpunkt S ist höchster Punkt und liegt im Ursprung $S(0\!\,|\!\,0)$ Für a < -1 ist der Graph im Vergleich zur Normalparabel gestreckt Für a > -1 ist der Graph im Vergleich zur Normalparabel gestaucht

STATION 3: Auswirkungen des Vorfaktors a auf einen Blick

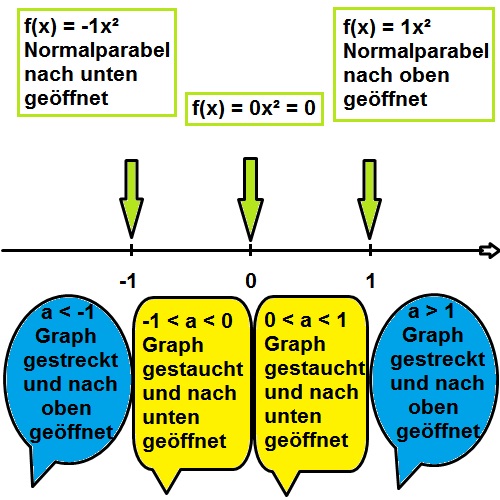
Da das nun einige Eigenschaften sowohl für den positiven, als auch für den negativen Vorfaktor a waren, wollen wir diese mal zusammenfassen. Dabei soll dir die folgende Grafik helfen. Du wirst feststellen, es ist gar nicht so schwer!!

Aufgabe:

Versuche mit Hilfe der Grafik und deinem bisherigen Wissen die richtigen Kombinationen zu finden!

	Vorgabe	Passendes Puzzleteil
1.	Vorfaktor a ist negativ	Nach unten geöffnete Normalparabel
2.	a < -1	Graph ist gestreckt
3.	Scheitelpunkt S für negativen Parameter a	Scheitelpunkt ist höchster Punkt und liegt im Ursprung [0, 0]
4.	0 > a > -1	Graph ist gestaucht
5.	Vorfaktor a ist positiv	Nach oben geöffnete Normalparabel
6.	0 < a < 1	Graph ist gestaucht
7.	Scheitelpunkt S für positiven Parameter a	Scheitelpunkt ist tiefster Punkt und liegt im Ursprung [0, 0]
8.	a > 1	Graph ist gestreckt
9.	Der Vorfaktor a bewirkt eine…	Streckung oder Stauchung der Normalparabel

STATION 4: Aufstellen der Funktionsgleichung

Bisher hast du den Wert des Vorfaktors a an der Grafik ablesen können. Nun wollen wir mal schauen, wie man anhand eines Graphen, den Parameter a bestimmt. Wir betrachten hierfür zunächst den Spezialfall, dass die Parabel weder in x-Richtung noch in y-Richtung verschoben wird.

Bearbeite die folgende Aufgabe und versuche die Vorgehensweise zum Bestimmen des Parameters a zu erkennen.

Quadratische Funktion f(x) = ax², für positiven und negativen Parameter a:

Hinweis und Aufgaben:

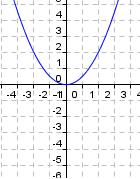
1. Gehe vom Scheitelpunkt aus eine Einheit nach rechts oder links auf der x-Achse. Wie viele Einheiten musst du in y-Richtung gehen um die Parabelkurve zu erreichen? (!2) (1) (!3) 2. Bediene nun den Schieberegler und stelle a = 2 ein. Gehe genauso vor wie in der Aufgabe 1. Um wie viele Einheiten muss man nun in y-Richtung gehen? (!3) (2) (!4) 3. Erkennst du schon ein Muster? Versuche folgendes Quiz zu lösen: Wenn man vom Scheitelpunkt aus eine Einheit nach rechts und 4 Einheiten nach oben geht, dann hat der Parameter den Wert: (!1) (!2) (!)3 (4) 4. Stelle nun den Schieberegler auf den Wert a = -2. Funktioniert das Ablesen des Parameters a an der Grafik genauso, wie bei positiven Werten von a? (!Nein) (JA) 5. Man geht vom Scheitelpunkt aus eine Einheit nach rechts und drei Einheiten nach unten! Wie lautet der Wert vom Parameter a?? (!1) (-3) (!3)

Merke Anleitung zur Bestimmung des Parameters a: Beginne beim Scheitelpunkt → Gehe eine Einheit nach rechts oder links auf der x-Achse → Bestimme die Anzahl der Einheiten nach oben oder unten bis zur Parabelkurve → Die Anzahl der Einheiten gibt den Wert vom Parameter a an Hat man die Einheiten nach oben abgezählt, so ist der Wert von a positiv Hat man die Einheiten nach unten abgezählt, so ist der Wert von a negativ

Um zu überprüfen, ob du die Vorgehensweise zum Finden des Parameters a verstanden hast, versuche die nächste Übung zu lösen.

Übung:

Bestimme die Funktionsgleichung wie gerade erlernt!

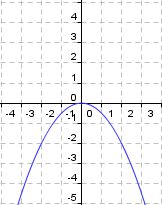
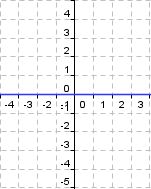
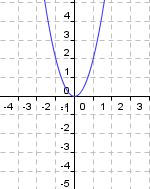
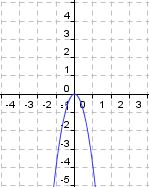
Ordne Bilder und Funktionsgleichungen richtig zu!

y = 0,5x2		y = 0x2		y = 2x2		y = -4x2		y = -0,5x2

STATION 5: Aufgaben zum Einüben der quadratischen Funktion f(x)$=$ax²

1. Aufgabe:

Für diese Aufgabe hast du eine Parabel aus dem Alltag vorgegeben. Du siehst hier den Ausschnitt einer Brücke. Beantworte zuerst die Frage und stelle dann den Graphen, durch Bedienen des Schiebereglers, richtig ein

Frage:

Was muss für den Parameter a gelten? (!er ist positiv) (er ist negativ) (!a < -1) (-1 < a < 0)

2. Aufgabe:

Gegeben ist die Funktionsvorschrift "f(x) = 0,5x².

In der folgenden Geogebra-Anwendung erkennst du die Punkte A, B, C und D. Diese Punkte können in y-Richtung verschoben werden. Ihr x-Wert hingegen ist vorgegeben. Überlege dir, welchen Wert der y-Wert einnimmt und bewege dorthin den Punkt. Überprüfe anschlieschließend durch Anklicken des Kontrollkästchens "Graph", ob all deine Punkte auf dem Graphen liegen, denn dann hast du die Aufgabe richtig gelöst!

3. Aufgabe:

Du hast die quadratische Funktion der Form f(x) = ax² gegeben.

Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt [2; 12] verläuft? (!1) (!2) (3) (!4)

Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt [3; 9] verläuft? (1) (!2) (!3) (!4)

Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt [4; 32] verläuft? (!1) (2) (!3) (!4)