Wiederholung wichtiger Formeln für die spätere Behandlung des Zylinders

Um später unseren neuen Körper "Zylinder" behandeln zu können, müssen wir zuerst einige schon gelernte Formeln und Bezeichnungen wiederholen. Dies kannst du in dem folgenden Lernpfad tun. Du benötigst dazu dein Schulheft, Stifte, Zirkel und eventuell deinen Taschenrechner.

1. Aufgabe

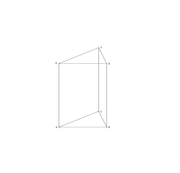
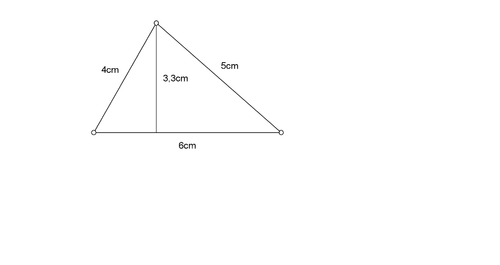
Hier siehst du ein dreiseitiges Prisma. Diesen Körper hast du bereits in der 7. Klasse kennengelernt.

Im folgenden Quiz kannst du dein Wissen zum Prisma überprüfen (manchmal gibt es auch zwei Lösungen!):

Wie viele Ecken hat ein dreiseitiges Prisma?

1. 8
2. 7
3. 9
4. 6

Welche Formen könnte man in der Mantelfläche finden?

1. Dreiecke
2. Kreise
3. Rechtecke
4. Quadrate

Aus wie vielen Seiten besteht die Oberfläche?

1. 4
2. 6
3. 5
4. 8

Was für eine Form hat die Grundfläche dreiseitiger Prismen?

1. Rechteck
2. Dreieck
3. Quadrat
4. Kreis

prüfen!

2. Aufgabe

Nun versuche die Paare richtig zusammen zufügen:

Mantelfläche des Prismas

Oberfläche des PrismasGrund- und Deckfläche des Prismas

3. Aufgabe

Nun haben wir die Bezeichnungen und Eigenschaften des dreiseitigen Prismas wiederholt, was uns noch fehlt, sind die Formeln zur Berechnung der Oberfläche, der Mantelfläche und des Volumens. Darum werden wir uns jetzt kümmern.

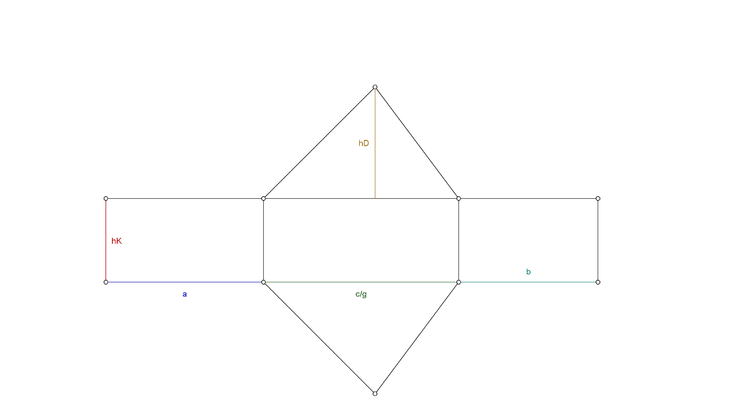
Hier siehst du ein Netz von einem Prisma. Die entsprechenden Bezeichnungen stehen auch schon da.
Vervollständige nun folgende Sätze:

Die Mantelfläche besteht aus drei                     . Den Flächeninhalt eines Rechtecks berechnet man, indem man die                     und die                     miteinander                     . Die Längen der Rechtecke sind in unserem Netz mit                     ,                     und                     bezeichnet. Die Breite entspricht bei uns                     . Um die Mantelfläche zu berechnen, kann man entweder die Flächeninhalte der einzelnen Rechtecke                     , oder man bildet ein großes Rechteck aus den drei kleinen. Hierfür addieren wir die                     der drei kleinen Rechtecke und                     dieses Ergebnis mit der Breite                     . Die Oberfläche des Prismas setzt sich zusammen aus der                     und der doppelten                     . Unsere Grundfläche ist ein                     . Die Fläche eines Dreiecks berechnen wir, indem wir die Grundseite                     mit der Höhe des Dreiecks                     multiplizieren und das Ergebnis durch                     teilen.

hKc/gmultipliziertbRechteckenaddierena2DreieckBreiteLängemultiplizierenghDLängenMantelflächeGrundflächehK

Nun können wir die Formeln für die Mantelfläche und die Oberfläche zusammentragen:

Mantelfläche $M=(a+b+c)*hK$

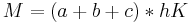
Oberfläche $O=2*G+M=2*\frac{g*hD}{2}+M$

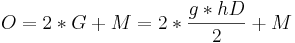
Das Volumen eines Körpers ist immer "Grundfläche mal Körperhöhe". In unserem Fall:

Volumen des Prismas $V=G*hK=\frac{g*hD}{2}*hK$

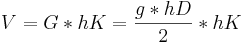
Übertrage diese drei Formeln bitte in dein Schulheft unter der Überschrift "Berechnungen am Prisma".

4. Aufgabe

Löse folgende Aufgaben bitte in deinem Schulheft. Wenn du das geschafft hast, kannst du dir bei mir ein Lösungsblatt abholen.

a)Die folgende Fläche ist die Grundfläche eines Prismas mit der Körperhöhe 8cm. Berechne M, O und V.

b) Die Mantelfläche eines geraden Prismas (Körperhöhe 32cm) beträgt 272cm². Wie lange ist der Umfang der Grundfläche?

c) Ein dreiseitiges Prisma hat als Grundfläche ein gleichseitiges Dreieck mit der Seitenlänge 4cm. Die Höhe des Körpers beträgt 5cm. Zeichne ein netz des Prismas und berechne dann Volumen und Oberfläche.