Geometrie: Trigonometrie: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| Zeile 31: | Zeile 31: | ||
| − | '''<math>\sin (\alpha) \approx 0{,}86603 </math> '''( | + | '''<math>\sin (\alpha) \approx 0{,}86603 </math> '''(<math>\alpha = 120° </math>) (!<math>\alpha = 150° </math>) (!<math>\alpha = 20° </math>) |
| − | '''<math>\ | + | '''<math>\cos (\alpha) = - 0{,}5 </math> '''(!<math>\approx 1</math>) (!0) (0,5) |
'''<math>\sin (\alpha) = a </math> '''(!2,5) (!0) (1) | '''<math>\sin (\alpha) = a </math> '''(!2,5) (!0) (1) | ||
Version vom 26. Juni 2009, 16:15 Uhr
Welche Werte stimmen? Wenn du die Antwort nicht aus dem Kopf weißt, kannst du das Maß mit Hilfe der GeoGebra-Anwendung herausfinden, indem du den Punkt C bewegst.
cos 0° = (1) (!0) (!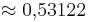 )
)
sin 30° = (!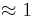 ) (!0) (0,5)
) (!0) (0,5)
tan 45° = (!2,5) (!0) (1)
cos 60° = (0,5) (!0) (!1)
sin 45° = (!0,5) (!1) (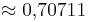 )
)
sin 90° = (1) (!0) (!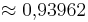 )
)
tan 30° = (!1) (!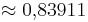 ) (
) (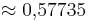 )
)
tan 0° = (!0,5) (0) (!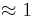 )
)
cos 90° = (!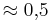 ) (0) (!1)
) (0) (!1)
Versuche nun, den jeweiligen Winkel herauszufinden. Benutze wieder die GeoGebra-Anwendung, wenn du dir unsicher bist.
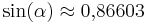 (
(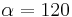 ) (!
) (!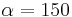 ) (!
) (!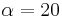 )
)
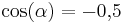 (!
(!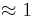 ) (!0) (0,5)
) (!0) (0,5)
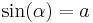 (!2,5) (!0) (1)
(!2,5) (!0) (1)
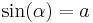 (0,5) (!0) (!1)
(0,5) (!0) (!1)
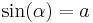 (!0,5) (!1) (
(!0,5) (!1) (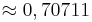 )
)
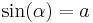 (1) (!0) (!
(1) (!0) (!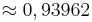 )
)
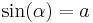 (!1) (!
(!1) (!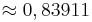 ) (
) (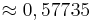 )
)
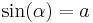 (!0,5) (0) (!
(!0,5) (0) (!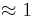 )
)
cos 90° = (!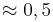 ) (0) (!1)
) (0) (!1)

