Ein- und zweistufige Zufallsexperimente: Unterschied zwischen den Versionen
K |
K (Karl Kirst verschob Seite Ein- und zweistufige Zufallsexperimente nach Lernpfade/Digitaler Test zur Stochastik der Sekundarstufe 1/Ein- und zweistufige Zufallsexperimente, ohne dabei eine Weiterleitung anzulegen) |
Aktuelle Version vom 13. April 2017, 23:11 Uhr
Aufgabe 1
- Du kaufst dir für dein Fahrrad ein neues Schloss, das mit einer Zahlenkombination gesichert ist.
Es hat zwei Zahlenräder, an denen jeweils die Ziffern 1 bis 3 eingestellt werden können - a) Wieviele Kombinationsmöglichkeiten hast du, um dein Zahlenschloss einzustellen?
Um das Zahlenschloss für mein Fahrrad einzustellen, gibt es 9 (Trage hier deine errechnete Zahl ein) Kombinationsmöglichkeiten.
- b) Wie lange würde ein Fahrraddieb brauchen, wenn er alle Möglichkeiten ausprobieren muss und er für das Einstelle pro Kombination 23 Sekunden Zeit braucht.
Kreuze an (Es können auch mehrere Antworten richtig sein)
(!109 Sekunden) (!5 Minuten 38 Sekunden) (207 Sekunden) (!454 Sekunden) (3 Minuten 27 Sekunden)
- c) Ordne die gesamten Kombinationsmöglichkeiten den richtigen Schlössern zu:
| Schloss mit 2 Zahlenrädern, 1 und 2 als mögliche Ziffern | {1;1} | {1;2} | {2;1} | {2;2} | |||||
| Schloss mit 2 Zahlenrädern, 3; 4 und 5 als mögliche Ziffern | {3;3} | {3;4} | {3;5} | {4;3} | {4;4} | {4;5} | {5;3} | {5;4} | {5;5} |
| Schloss mit 3 Zahlenrädern, 0 und 9 als mögliche Ziffern | {0;0;0} | {0;0;9} | {0;9;0} | {0;9;9} | {9;0;0} | {9;0;9} | {9;9;0} | {9;9;9} |
- d) Wenn du die Auswahl hättest, für welches Schloss würdest du dich entscheiden? Welches Schloss ist jeweils sicherer?
1. (!Schloss mit 3 Zahlenrädern, 2 und 3 als mögliche Ziffern) (Schloss mit 2 Zahlenrädern, 4; 5 und 6 als mögliche Ziffern) (!beide Schlösser sind gleich sicher)
2. (Schloss mit 5 Zahlenrädern, 0;1;2 und 3 als mögliche Ziffern) (!Schloss mit 6 Zahlenrädern, 6; 7 und 8 als mögliche Ziffern) (!beide Schlösser sind gleich sicher)
3. (!Schloss mit 4 Zahlenrädern, 3 und 4 als mögliche Ziffern) (!Schloss mit 2 Zahlenrädern, 5; 6; 7 und 8 als mögliche Ziffern) (beide Schlösser sind gleich sicher)
Aufgabe 2
- Du wirfst mit zwei Würfeln.
- a) Welche Zahlenkombinationen kannst du würfeln und wieviele sind es?
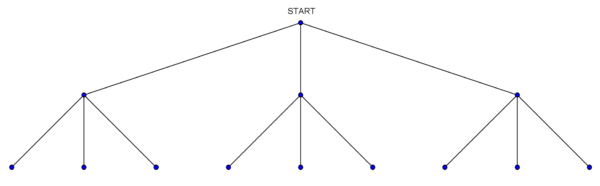
Damit dir das Abzählen leichter fällt, ist es sinnvoll zu diesem Experiment ein Baumdiagramm zu zeichnen.
- Hier kannst du dein Baumdiagramm kontrollieren:
- Klicke im folgenden alle möglichen Zahlenkombinationen an:
({1;1}) ({1;2}) ({1;3}) ({1;4}) ({1;5}) ({1;6}) ({2;1}) ({2;2}) ({2;3}) ({2;4}) ({2;5}) ({2;6}) ({3;1}) ({3;2}) ({3;3}) ({3;4}) ({3;5}) ({3;6}) ({4;1}) ({4;2}) ({4;3}) ({4;4}) ({4;5}) ({4;6}) ({5;1}) ({5;2}) ({5;3}) ({5;4}) ({5;5}) ({5;6}) ({6;1}) ({6;2}) ({6;3}) ({6;4}) ({6;5}) ({6;6}) (!{1;7}) (!{2;0}) (!{5;9}) (!{3;8}) (!{0;1}) (!{9;7}) (!{2;7}) (!{4;0}) (!{7;5}) (!{8;0}) (!{4;8}) (!{0;5}) (!{6;7}) (!{7;7})
Insgesamt gibt es also sechsunddreißig mögliche Zahlenkombinationen.
- b) Wie oft sind die einzelnen Augensummen möglich?
Um das herauszufinden, ordne die jeweiligen Zahlenkombinationen der dazugehörigen Augenzahl zu.
| Augenzahl: 2 | {1;1} | |||||
| Augenzahl: 3 | {1;2} | {2;1} | ||||
| Augenzahl: 4 | {1;3} | {2;2} | {3;1} | |||
| Augenzahl: 5 | {4;1} | {3;2} | {2;3} | {1;4} | ||
| Augenzahl: 6 | {5;1} | {4;2} | {3;3} | {2;4} | {1;5} | |
| Augenzahl: 7 | {6;1} | {5;2} | {4;3} | {3;4} | {2;5} | {1;6} |
| Augenzahl: 8 | {6;2} | {5;3} | {4;4} | {3;5} | {2;6} | |
| Augenzahl: 9 | {6;3} | {5;4} | {4;5} | {3;6} | ||
| Augenzahl: 10 | {6;4} | {5;5} | {4;6} | |||
| Augenzahl: 11 | {6;5} | {5;6} | ||||
| Augenzahl: 12 | {6;6} |
- Hast du die Zahlenpaare den Augenzahlen richtig zugeordnen, dann fülle die folgenden Lücken:
Die Augensumme 2 und 12 können jeweils durch eine Zahlenkombination erreicht werden, die Augensumme 3 und 11 durch jeweils zwei. Je drei Zahlenpaare führen zur Augensumme 4 und 10, sowie je vier Zahlenpaare zu den Augensummen 5 und 9 führen. 6 und 8 als Augensumme erhält man mithilfe von jeweils fünf Zahlenkombinationen. Die Augensumme 7 wird durch sechs verschiedene Kombinationen erreicht.
Aufgabe 3
- In einem Gefäß befinden sich beliebig viele rote und grüne Kugeln. Vier Schüler ziehen nacheinander drei Kugeln aus dem Gefäß,
ohne sie wieder zurückzulegen.
- a) Wieviele rote und grüne Kugeln können sich in dem Gefäß befinden? Kreuze die richtigen Antworten an:
(!zwei rote und eine grüne Kugel) (!höchstens 2 rote Kugeln) (mindestens 3 rote Kugeln) (!nur rote Kugeln) (!nur grüne Kugeln) (mindestens eine grüne Kugel) (es können auch mehr als eine grüne Kugeln im Gefäß sein) (es können auch mehr als drei rote Kugeln im Gefäß sein)
- b) Es befinden sich insgesamt 6 Kugeln in dem Gefäß. Wieviele Kugeln können rot und wieviel können grün sein?
In dem Gefäß befindet sich mindestens eine, jedoch aber höchstens drei grüne Kugeln. Außerdem sind es mindestens drei und höchstens fünf rote Kugeln.
Aufgabe 4
- Das Spiel "Mäxchen" ist ein beliebtes Würfelspiel. Dabei werden zwei Würfel gleichzeitig gewürfelt.
Aus den beiden gewürfelten Augenzahlen wird die größere Zweistellige Zahl gebildet. (Würfelt man beispielsweise eine 3 und eine 4, dann entsteht die Zahl 43).
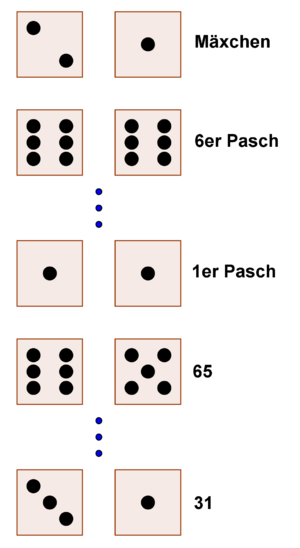
Es wird reihum gewürfelt und der eigene Wurf muss höher sein, als der des Vorgängers. Der höchste Wurf ist "Mäxchen", also eine 2 und eine 1.
Dann folgen alle Pasche von 6er nach 1er und dann alle anderen zweistelligen Zahlen. Als kleine Hilestellung für die Reihenfolge soll folgendes Bild dienen:
- a) Kreuze alle möglichen zweistelligen Zahlen an, die du während des Mäxchenspiels würfeln kannst.
(21) (66) (55) (44) (33) (22) (11) (65) (64) (63) (62) (61) (54) (53) (52) (51) (43) (42) (41) (32) (31) (!56) (!46) (!35) (!26) (!57) (!38) (!24) (!71) (!45) (!36) (!34) (!25) (!84) (!82) (!40) (!91)
- b) Dein Vordermann sagt, dass er 52 gewürfelt hat. Schätze deine Chancen ab, diesen Wurf zu übertreffen.
Die Chancen für mich stehen eher (!schlecht) (gut)
 Zurück
Zurück
