Auswerten und Interpretieren von Daten

Aufgabe 1

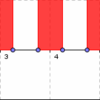
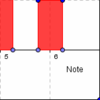
Die Abbildungen zeigen die Verteilungen der Noten in den ersten beiden Mathematikschulaufgaben der Klasse 5a

a) Wieviele Schüler haben in der ersten bzw. der zweiten Schulaufgabe die Note 3?

In der 1. Schulaufgabe haben elf Schüler eine 3 geschrieben und in der 2. Schulaufgabe neun.

b) In einer Schulaufgabe war ein Schüler krank und konnte deshalb nicht mitschreiben.

Bei welcher Schulaufgabe war das der Fall? (bei der ersten) (!bei der zweiten) (!bei keiner)

Aufgabe 2

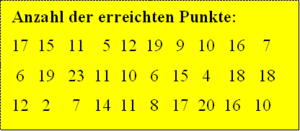
Die Anzahl der erreichten Punkte der einzelnen Schüler in der dritten Schulaufgabe der Klasse 5a
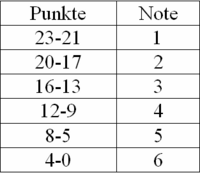
sind in einer Liste zusammengefasst. Daneben findest du den Notenschlüssel

a) Fülle die Häufigkeitstabelle

Häufigkeiten
Ordne die Anzahl den jeweiligen Noten zu und umgekehrt.

Note 1	1 mal
Note 2	7 mal
Note 3	5 mal
Note 4	9 mal
Note 5	6 mal
Note 6	2 mal

b) In welcher der drei Schulaufgaben (erste und zweite Schulaufgabe siehe Aufgabe 1) gab es mehr bessere (Note 1-3) als schlechtere (Note 4-6) Noten?

In welcher gab es mehr bessere Noten? (1. Schulaufgabe) (!2. Schulaufgabe) (!3. Schulaufgabe)

c) Füge das folgende Puzzle zusammen. Du brauchst es dann für Aufgabe d)

d) Versuche die Fragen zu den drei Schulaufgaben zu beantworten. Es können auch mehrere Antworten richtig sein.

Wieviele Kinder sind in der Klasse 5a? (!28) (!29) (!30) (31) (!32)

In welchen Schulaufgaben waren Kinder krank? (1.Schulaufgabe) (!2.Schulaufgabe) (3.Schulaufgabe) (!bei keiner)

In welcher Schulaufgabe wurden die meisten 5er geschrieben? (!1.Schulaufgabe) (!2.Schulaufgabe) (3.Schulaufgabe)

Welche Schulaufgabe ist deiner Meinung nach am besten ausgefallen? (1.Schulaufgabe) (!2.Schulaufgabe) (!3.Schulaufgabe)

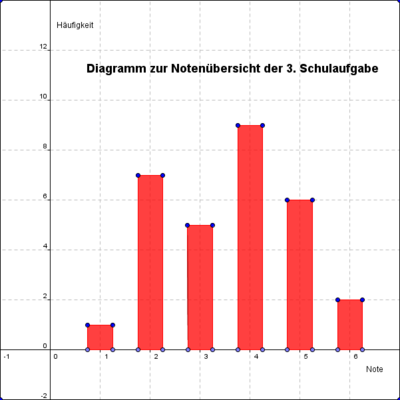
Welche Note hatten die meisten Schüler in der 3. Schulaufgabe? (!Note 1) (!Note 2) (!Note 3) (Note 4) (!Note 5) (!Note 6)

Aufgabe 3

Definitionen: Es sind insgesamt vier Begriffe im Buchstabensalat versteckt, die die Antworten auf die jeweiligen Fragen bilden.

1. Wie nennt man das arithmetische Mittel noch?

2. Wie heißt die Differenz aus dem Maximum und dem Minimum einer Liste mit bestimmten Werten?

3. Wie nennt man den Wert, der in der Mitte steht, wenn die Daten der Größe nach geordnet werden?

4. Wie heißt der Wert, der in einer Liste am häufigsten auftritt?

Finde die Wörter! (Waagrecht (von links nach rechts), senkrecht (von oben nach unten) und schräg (von links unten nach rechts oben oder von oben links nach unten rechts), gefundene Wörter werden grün markiert)

Durchschnitt

Spannweite

Zentralwert

Modalwert

Aufgabe 4

Anna, Thomas und Katja sind 11 Jahre alt, Michael ist 12, Verena ist 13 und Laura und Christian sind 10 Jahre alt. Finde die zusammengehörenden Terzette.

stochastische Kenngrößen
Die drei zusammenpassenden Karten bestehen aus der Rechnung bzw dem Lösungsweg, dem Ergebnis und dem mathematischen Begriff

	cirka 11,14	arithmetisches Mittel
12-10	2	Spannweite
	11	Modalwert
	11	Zentralwert

Aufgabe 5

Nimm Stellung zu folgenden Aussagen. Überlege dir jeweils ein Beispiel, das deine Aussage belegt.

a) Das arithmetische Mittel, der Zentralwert und der Modalwert können nicht gleich sein. (!stimmt) (stimmt nicht)

Lösungsvorschlag a)

b) Je größer die Spannweite, desto größer der Modalwert. (!stimmt) (stimmt nicht)

Lösungsvorschlag b)

c) Wenn du einen Wert einer Datenmenge änderst, ändert sich auch immer die Spannweite. (!stimmt) (stimmt nicht)

Lösungsvorschlag c)

d) Streicht man einen beliebigen Wert aus einer Datenmenge, so muss sich das arithmetische Mittel nicht zwangsläufig ändern. (stimmt) (!stimmt nicht)

Lösungsvorschlag d)

$\Leftarrow$ Zurück