Netz und Oberfläche der Pyramide
2.1 Oberfläche der Pyramide
Die Vereinigung der Grundfläche mit der Mantelfläche bezeichnet man als die Oberfläche der Pyramide.
Zur Betrachtung und Berechnung der Oberfläche ist es deshalb zunächst sinnvoll, die Grundfläche,
die Mantelfläche als auch das Netz der Pyramide näher kennenzulernen. Das Netz stellt nämlich die Oberfläche in zweidimensionaler Ebene dar.
2.1.1 Die Grundfläche der Pyramide
Wie viele andere Körper hat auch die Pyramide eine Grundfläche (Die Kugel beispielsweise hat keine Grundfläche).
Die Grundfläche hat immer die Form eines n-Ecks, also sind als Grundfläche Quadrate, Rechtecke, Dreiecke oder auch 8-Ecke
möglich.
Kurz: Die Grundfläche der Pyramide besitzt immer mindestens drei Ecken.
Als Grundfläche sind Kreise ausgeschlossen, denn in diesem Fall würde ein klassischer Kegel anstatt einer Pyramide entstehen.
Folgende Flächen kommen als Grundfläche in Frage, jedoch haben sich Fehler eingeschlichen.
Aus welchen Grundflächen kann keine Pyramide entstehen?
Folgende Flächen sind keine Pyramidengrundflächen: (#1) (!#2) (!#3) (!#4) (#5) (!#6)
2.1.2 Die Mantelfläche der Pyramide
Die Mantelfläche der Pyramide besteht immer aus Dreiecken.
Um die Dreiecksflächen berechnen zu können, benötigen wir nach der Formel 1/2 * g * h ("Einhalb mal Grundseite mal Höhe")
neben den Längen der Grundkanten (Im Dreieck entspricht dies der Grundseite) auch jeweils die Dreieckshöhen hs!
Diese sind meist nicht gegeben und auch ohne Weiteres nicht berechenbar.
Um die Dreieckshöhen hs berechnen zu können, machen wir Gebrauch von sogenannten Stützdreiecken!
Im folgenden Applet könnt ihr einige Stützdreiecke ein- und ausblenden.
 Für die darauf folgenden Aufgaben und deren Nebenrechnungen benötigst du Stift, Papier und eventuell deinen Taschenrechner; die Ergebnisse trägt du dann weiter unten zur Überprüfung ein.
Für die darauf folgenden Aufgaben und deren Nebenrechnungen benötigst du Stift, Papier und eventuell deinen Taschenrechner; die Ergebnisse trägt du dann weiter unten zur Überprüfung ein.
Die Grundfläche einer Pyramide ABCDS ist die Raute ABCD. Die Spitze S befindet sich senkrecht über dem Schnittpunkt M der Diagonalen der Grundfläche.
Es gilt: ![]() = 9 cm;
= 9 cm; ![]() = 7 cm;
= 7 cm; ![]() = 8 cm
= 8 cm
Endergebnisse werden auf zwei Stellen nach dem Komma gerundet!
Aufgaben (Hinweis: Blende die Stützdreiecke oben ein/aus):
- Fertige eine Skizze der Pyramide an und beschrifte die Eckpunkte, sowie die bekannten Längen
- Berechne alle Innenwinkel und Seitenlängen der Raute (= Grundfläche)
- Berechne die Mantelfläche ( Lösungsansatz )
- Berechne die Oberfläche
Nun gebe deine Ergebnisse unten ein, und überprüfe inwieweit du die Aufgaben richtig gelöst hast:
Die Seitenlängen der Raute betragen 15,75 (in cm).
Die Innenwinkel der Raute betragen jeweils 75,74° und 104,26 (in °, auf zwei Stellen nach dem Komma gerundet).
Die Höhe ![]() des Dreiecks BCS beträgt8,46 (in cm, auf zwei Stellen nach dem Komma gerundet).
des Dreiecks BCS beträgt8,46 (in cm, auf zwei Stellen nach dem Komma gerundet).
Die anderen drei Dreieckshöhen sind gleich (gleich/unterschiedlich) groß, weil alle vier Dreiecke kongruent sind.
Die Fläche des Dreiecks BCS beträgt 66,62 (in cm², auf zwei Stellen nach dem Komma gerundet).
Die Mantelfläche der Pyramide beträgt somit 266,48 (in cm², auf zwei Stellen nach dem Komma gerundet).
Die Oberfläche setzt sich zusammen aus Grundfläche und Mantelfläche und beträgt bei dieser Pyramide 297,98 (in cm²).
2.2 Netz der Pyramide
Schneidet man eine Pyramide entlang der Seitenkanten auf und klappt die Seitenflächen
in die Ebene der Grundfläche, so erhält man das Netz der Pyramide.
Im folgenden GeoGebra-Applet seht ihr eine Pyramide ABCD mit der Spitze S von oben.
Verschiebt die vier Regler außerhalb der Pyramide, um die Pyramide "aufzuklappen",
so dass das Netz der Pyramide entsteht.
Das blaue Feld entspricht der... (!Mantelfläche) (!Oberfläche) (Grundfläche) (!Grundkante)
Die grünen Felder zusammen ergeben die... (!Oberfläche) (Mantelfläche) (!Seitenkanten) (!Grundfläche)
Die Höhe hs, die am Anfang des Applets zu sehen ist, ist die Höhe der... (Seitenfläche) (!Pyramide) (Seitenflächen)
Die Oberfläche ergibt sich wiefolgt: (blaues Feld + alle grünen Felder) (!alle grünen Felder) (!nur das blaue Feld) (!blaues Feld + ein grünes Feld)
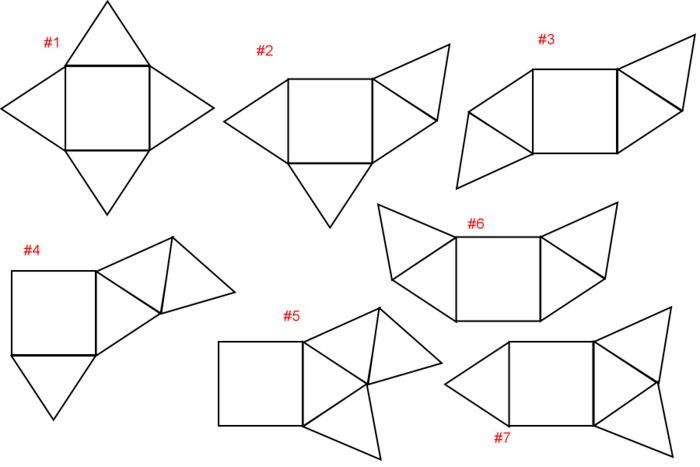
Weitere Pyramidennetze
Ein Pyramidennetz kann auch anders aussehen, wenn man nicht nur den Seitenkanten entlang aufschneidet, sondern auch entlang der Grundkanten.
Dabei ist zu beachten, dass keine Dreiecksfläche komplett abgetrennt wird, denn das Netz der Pyramide muss immer eine zusammenhängende Fläche sein, die wieder zu einer vollständigen Pyramide gefaltet werden kann.
Hier unten siehst du oben links (#1) das bereits bekannte Netz einer geraden und quadratischen Pyramide, das wir durch aufschneiden aller Seitenkanten erhalten.
Auch bei dieser Aufgabe hat sich ein Fehler eingeschlichen!
Falte nun gedanklich die verschiedenen Netze zu einer Pyramide und finde heraus, welches Netz keine Pyramide ergibt!
 Fällt dir das gedankliche Falten schwer? Dann zeichne die Netze in geeigneter Größe. Schneide die Netze aus und finde durch Falten heraus, welches Netz kein Pyramidennetz ist.
Fällt dir das gedankliche Falten schwer? Dann zeichne die Netze in geeigneter Größe. Schneide die Netze aus und finde durch Falten heraus, welches Netz kein Pyramidennetz ist.
Welches Netz ist deiner Meinung nach falsch?
Das Pyramidennetz #6 (trage die Zahl ohne '#' ein) ist falsch. Man erhält durch bloßes Falten keine Pyramide.